Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét (O) có
ΔABC nội tiếp
AB là đường kính
=>ΔABC vuông tại C
=>BC vuông góc AC
Xét ΔKAB vuông tại A có AC là đường cao
nên BC*BK=BA^2=4*R^2

a: Xét tứ giác AEMO có
\(\widehat{EAO}+\widehat{EMO}=180^0\)
Do đó: AEMO là tứ giác nội tiếp

2: Xét tứ giác OBCD có
\(\widehat{OBC}+\widehat{ODC}=180^0\)
Do đó: OBCD là tứ giác nội tiếp
hay O,B,C,D cùng thuộc một đường tròn

a: Xét tứ giác CAOM có góc CAO+góc CMO=180 độ
nên CAOM là tứ giác nội tiếp
Tâm là trung điểm của OC
b: Xét (O) có
CM,CA là các tiếp tuyến
nên CM=CA và OC là phân giác của góc MOA(1)
Xét (O) có
DM,DB là các tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
AC+BD=CM+MD=CD

a: Xét tứ giác OBDM có
góc OBD+góc OMD=180 độ
=>OBDM là tư giác nội tiếp
c: Xét ΔKOB và ΔKFE có
góc KOB=góc KFE
góc OKB=góc FKE
=>ΔKOB đồng dạng với ΔKFE
=>KO/KF=KB/KE
=>KO*KE=KB*KF

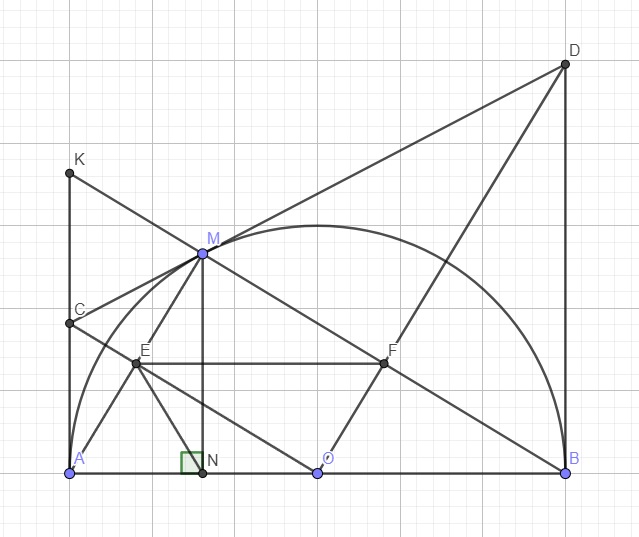
C là giao điểm 2 tiếp tuyến tại A và M \(\Rightarrow OC\) là trung trực AM
\(\Rightarrow E\) là trung điểm AM
Tương tự ta có OD là trung trực BM \(\Rightarrow F\) là trung điểm BM
\(\Rightarrow EF\) là đường trung bình tam giác ABM
\(\Rightarrow EF||AB\Rightarrow ONEF\) là hình thang (1)
Lại có O là trung điểm AB \(\Rightarrow OF\) là đường trung bình tam giác ABM
\(\Rightarrow OF=\dfrac{1}{2}AM=AE\)
Mà \(OF||AE\) (cùng vuông góc BM)
\(\Rightarrow AEFO\) là hình bình hành \(\Rightarrow\widehat{OFE}=\widehat{OAE}\)
Mà \(EN=AE=\dfrac{1}{2}AM\Rightarrow\Delta AEN\) cân tại E \(\Rightarrow\widehat{OAE}=\widehat{ANE}\)
\(\widehat{ANE}+\widehat{ONE}=180^0\Rightarrow\widehat{OFE}+\widehat{ONE}=180^0\)
Lại có \(\widehat{ONE}+\widehat{NEF}=180^0\) (2 góc trong cùng phía)
\(\Rightarrow\widehat{OFE}=\widehat{NEF}\)
\(\Rightarrow ONEF\) là hình thang cân
a: góc DAO+góc DMO=90+90=180 độ
=>DAOM nội tiếp đường tròn (O)
b: Xét (O) có
DA,DM là tiếp tuyến
=>DA=DM
mà OA=OM
nên OD là trung trực của AM
=>OD vuông góc AM tại H
ΔOMD vuông tại M có MH là đường cao
nên OH*OD=OM^2
=>OH*OD=R^2