Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

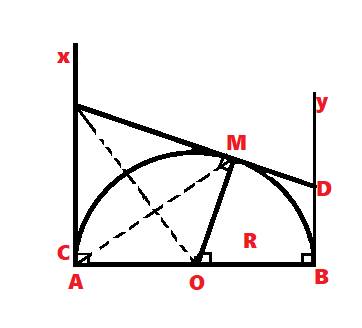
a: Xét (O) có
CA,CM là tiếp tuyến
Do đó: CA=CM và OC là phân giác của \(\widehat{MOA}\)
=>\(\widehat{MOA}=2\cdot\widehat{MOC}\)
CA=CM
=>C nằm trên đường trung trực của AM(1)
OA=OM
=>O nằm trên đường trung trực của AM(2)
Từ (1) và (2) suy ra OC là đường trung trực của AM
=>OC\(\perp\)AM
b: Xét tứ giác CAOM có \(\widehat{CAO}+\widehat{CMO}=90^0+90^0=180^0\)
nên CAOM là tứ giác nội tiếp
=>C,A,O,M cùng thuộc một đường tròn
c: Xét (O) có
DM,DB là tiếp tuyến
Do đó: OD là phân giác của góc MOB và DM=DB
=>\(\widehat{MOB}=2\cdot\widehat{MOD}\)
\(\widehat{MOA}+\widehat{MOB}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{MOC}+\widehat{MOD}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)
=>ΔCOD vuông tại O
Xét ΔOCD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
mà MC=CA và DM=DB
nên \(CA\cdot DB=OM^2=R^2\)

a: Xét (O) có
CM,CA là các tiếp tuyến
nen CM=CA và OC là phân giác của góc MOA(1)
Xét (O) có
DM.DB là các tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
CD=CM+MD
=>CD=AC+BD
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
b: AC*BD=CM*MD=OM^2=R^2

Trả lời hộ mình cái xin. mình đã 2 năm ko on r giờ mới on lại :(((.Xin mọi người trả lời giúp mình :(((


1/ Do EF//AD nên \(EF\perp AB\)
Theo tính chất đường kính dây cung ta có AB đi qua trung điểm EF hay AB là trung trực EF.
Vậy thì AE = AF; BE = BF.
2/ Ta thấy hai tam giác vuông DAO và DCO có chung cạnh huyền DO nên DAOC là tứ giác nội tiếp đường tròn đường kính DO.
3/Xét tam giác DEC và DCB có :
Góc D chung
\(\widehat{DCE}=\widehat{DBC}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung)
\(\Rightarrow\Delta DEC\sim\Delta DCB\left(g-g\right)\)
\(\Rightarrow\frac{DE}{DC}=\frac{DC}{DB}\Rightarrow DC^2=DE.DB\)
4/ Vì \(\Delta DEC\sim\Delta DCB\Rightarrow\frac{EC}{BC}=\frac{DC}{DB}\Rightarrow EC=\frac{BC.DC}{DB}\)
\(\Rightarrow AC.EC=\frac{AC.BC.DC}{DB}=\frac{2S_{ABC}.DC}{DB}\)
Ta cần chứng minh AC.EC = AF.CH (*) hay \(\Rightarrow\frac{2S_{ABC}.DC}{CH}=AF.DB\Rightarrow\frac{2S_{ABC}.DC}{CH}=AE.DB\)
\(\Rightarrow AE.DB=AB.DC=AB.DA\) (**)
(**) đúng vì \(AE.DB=AB.DA\left(=S_{DAB}\right)\)
Vậy (*) đúng hay AF.CH = AC.EC
5/ Ta cần chứng minh KA = KD để suy ra KE là tiếp tuyến.
Kéo dài AE, cắt CH tại M .
Do DA // CH (Cùng vuông góc AB) nên \(\frac{AK}{CM}=\frac{KI}{IC}\)
và \(\frac{KD}{CH}=\frac{KI}{IC}\Rightarrow\frac{AK}{MC}=\frac{KD}{CH}\) (1)
Gọi P, J lần lượt là giao điểm của DP với CH và BC với AD.
\(\Rightarrow\frac{HP}{AD}=\frac{BP}{BD}=\frac{CP}{DJ}\) (2)
Xét tam giác ACJ vuông tại C, AD = DC nên DC là đường trung tuyến. Suy ra AD = DJ.
Từ (2) suy ra HP = PC.
Xét tam giác vuông AMH và PBH, ta có \(\widehat{AMH}=\widehat{HBP}\) (cạnh tương ứng vuông góc)
\(\Rightarrow\Delta AMH\sim\Delta PBH\left(g-g\right)\)
\(\Rightarrow\frac{MH}{BH}=\frac{AH}{PH}\Rightarrow\frac{MH}{AH}=\frac{BH}{PH}\)
\(\Rightarrow MH=\frac{AH.HB}{PH}=\frac{AH.HB}{\frac{CH}{2}}=\frac{2AH.HB}{CH}\) (3)
Do CH2 = AH.HB \(\Rightarrow\frac{2AH.HB}{CH}=2CH\)
Từ (3) \(\Rightarrow MH=2CH\Rightarrow CM=CH\)
Từ (1) ta có AK = KD
\(\Rightarrow\) KE là trung tuyến của tam giác vuông ADE \(\Rightarrow KA=KE\)
\(\Rightarrow\Delta OKA=\Delta OKE\left(c-c-c\right)\Rightarrow\widehat{KEO}=\widehat{KAO}=90^o\)
hay KE là tiếp tuyến của (O).