Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Điểm M ở đâu vậy bạn?
b: góc ONP=góc ONB+góc PNB
góc ANB=1/2*sđ cung AB=90 độ
=>BN vuông góc AK
=>BN//KC
=>góc ABN=góc ACK
=>góc ONB=góc ACK
Xét ΔKBC có
KP vừa là đường cao, vừa là trung tuyến
=>ΔKBC cân tại K
=>góc BKP=góc CKP
góc ONP=góc ONB+góc BNP
=góc ONB+góc BKP
=góc ONB+góc CKP
=góc OBN+góc NAB=90 độ
=>NP là tiếp tuyến của (O)

b: góc ONP=góc ONB+góc PNB
góc ANB=1/2*sđ cung AB=90 độ
=>BN vuông góc AK
=>BN//KC
=>góc ABN=góc ACK
=>góc ONB=góc ACK
Xét ΔKBC có
KP vừa là đường cao, vừa là trung tuyến
=>ΔKBC cân tại K
=>góc BKP=góc CKP
góc ONP=góc ONB+góc BNP
=góc ONB+góc BKP
=góc ONB+góc CKP
=góc OBN+góc NAB=90 độ
=>NP là tiếp tuyến của (O)
a: KNBP nội tiếp
=>góc PNK=góc PBK; góc PKN=180 độ-góc NBP
=>góc PNK=góc PCK
=>góc PNK=góc AKP
180 độ-góc NBP=góc ABN
=>180 độ-góc NBP=góc AKP
=>góc PNK=góc PKN
=>PK=PN

a: Xét (O) có
MP là tiếp tuyến
MB là tiếp tuyến
Do đó: MP=MB và OM là tia phân giác của góc POB(1)
Xét (O) có
NP là tiếp tuyến
NC là tiếp tuyến
Do đó: NP=NC và ON là tia phân giác của góc POC(2)
Ta có: MN=MP+PN
nên MN=MB+NC
b: Từ (1) và (2) suy ra \(\widehat{MON}=\dfrac{1}{2}\cdot\left(\widehat{POB}+\widehat{POC}\right)=\dfrac{1}{2}\cdot180^0=90^0\)

a/ Nối A với D ta có
\(\widehat{ADB}=90^o\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow AD\perp BC\)
=> H và D cùng nhìn AC dưới 1 góc vuông => AHDC là tứ giác nội tiếp
b/
Xét tg vuông ACO có
\(\widehat{ACO}+\widehat{AOC}=90^o\)
Ta có \(\widehat{ADH}+\widehat{EDB}=\widehat{ADB}=90^o\)
Xét tứ giác nội tiếp AHDC có
\(\widehat{ACO}=\widehat{ADH}\) (Góc nội tiếp cùng chắn cung AH)
\(\Rightarrow\widehat{AOC}=\widehat{EDB}\)
Xét tam giác EOH và tg EBD có
\(\widehat{BED}\) chung
\(\widehat{AOC}=\widehat{EDB}\)
=> tg EOH đồng dạng với tg EDB (g.g.g)
\(\Rightarrow\dfrac{EH}{EB}=\dfrac{EO}{ED}\Rightarrow EH.ED=EO.EB\)
a) Ta có \(\widehat{ADB}=90^0\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow\widehat{ADC}=90^0\)
Tứ giác \(AHDC\) có: \(\widehat{ADC}=\widehat{AHC}=90^0\) mà 2 góc này nội tiếp và chắn cung AC
\(\Rightarrow AHDC\) là tứ giác nội tiếp
b) Tứ giác \(AHDC\) nội tiếp \(\Rightarrow\widehat{ACO}=\widehat{ADE}\) (góc nội tiếp cùng chắn 1 cung)
Ta có: \(\widehat{EOH}=90^0-\widehat{ACO}=90^0-\widehat{ADE}=\widehat{EDB}\)
Xét \(\Delta EOH\) và \(\Delta EDB\) có:
\(\widehat{BED}\) chung
\(\widehat{EOH}=\widehat{EDB}\) (đã chứng minh)
\(\Rightarrow\Delta EOH\sim\Delta EDB\) (g.g) \(\Rightarrow\dfrac{EO}{EH}=\dfrac{ED}{EB}\Rightarrow EH.ED=EO.EB\)

AB cắt đường tròn ngoại tiếp tam giác AEK tại D
Vì AB là đường kính \(\Rightarrow\angle AMB=90\Rightarrow\angle EMB+\angle EHB=90+90=180\)
\(\Rightarrow EMBH\) nội tiếp \(\Rightarrow\angle KBD=\angle MBH=\angle AEH\)
Vì KEAD nội tiếp \(\Rightarrow\angle AEH=\angle KDB\Rightarrow\angle KBD=\angle KDB\)
\(\Rightarrow\Delta KDB\) cân tại K có KH là đường cao
\(\Rightarrow H\) là trung điểm BD mà B,H cố định \(\Rightarrow D\) cố định
Vì KEAD nội tiếp \(\Rightarrow I\in\) trung trực AD mà A,D cố định
\(\Rightarrow\) đpcm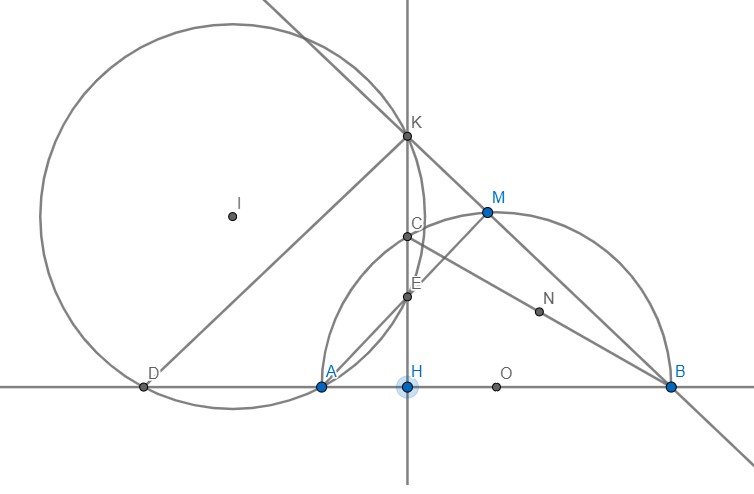

(Quá lực!!!)
Đầu tiên, hãy CM tam giác \(EAH\) và \(ABD\) đồng dạng.
Từ đó suy ra \(\frac{EA}{AB}=\frac{AH}{BD}\) hay \(\frac{EA}{OB}=\frac{AC}{BD}\).
Từ đây CM được tam giác \(EAC\) và \(OBD\) đồng dạng.
Suy ra \(\widehat{ECA}=\widehat{ODB}\). Do đó nếu gọi \(OD\) cắt \(EC\) tại \(L\) thì CM được \(OD⊥EC\).
-----
Đường tròn đường kính \(NC\) cắt \(EC\) tại \(F\) nghĩa là \(NF⊥EC\), hay \(NF\) song song với \(OD\).
Vậy \(NF\) chính là đường trung bình của tam giác \(AOD\), vậy \(NF\) qua trung điểm \(AO\) (là một điểm cố định) (đpcm)