Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mạng mẽo như gì, xin lỗi bạn hen
c, (O;R) có EM, AE là 2 tiếp tuyến cắt nhau => AE = EM, EO là phân giác của góc AEM
\(\Delta AEM\) có: AE = EM \(\Rightarrow\Delta AEM\)cân tại E có EO là phân giác của \(\hat{AEM}\)nên EO là đường cao \(\Rightarrow EO\perp AM\)
\(\Delta AMB\) nội tiếp (O), AB là đường cao nên \(\Delta AMB\) vuông tại M \(\Rightarrow AM\perp MB\)
Từ 2 điều trên \(\Rightarrow\)EO // MB \(\Rightarrow\)\(\hat{EOM}=\hat{ABM}\) (so le trong)
Dễ dàng chứng minh \(\Delta EMO \sim \Delta AMB (g-g)\)\(\Rightarrow\dfrac{EM}{OE}=\dfrac{AM}{AB}\Rightarrow EM.AB=AM.OE\)(1)
Chứng minh tương tự ta có: \(\Delta FMO \sim \Delta BMA (g-g)\)\(\Rightarrow\dfrac{OF}{MF}=\dfrac{AB}{BM}\Rightarrow OF.BM=AB.MF\)(2)
Cộng (1) và (2) ta có: \(AM.OE+OF.BM=AB.MF+EM.AB\)
\(=AB\left(MF+EM\right)=AB.EF\)

a: Xét ΔEAO và ΔEMO có
EA=EM
OA=OM
EO chung
Do đó: ΔEAO=ΔEMO
=>góc EMO=90 độ
=>EF là tiếp tuyến của (O)
b: Xét (O) có
FM,FB là các tiếp tuyến
nên OF là phân giác của góc MOB(1)
Ta có: ΔEAO=ΔEMO
nên góc AOE=góc MOE
=>OE là phân giác của góc MOA(2)
Từ(1) và (2) suy ra góc EOF=1/2*180=90 độ
=>ΔEOF vuông tại O

a: Xét tứ giác OBDM có
góc OBD+góc OMD=180 độ
=>OBDM là tư giác nội tiếp
c: Xét ΔKOB và ΔKFE có
góc KOB=góc KFE
góc OKB=góc FKE
=>ΔKOB đồng dạng với ΔKFE
=>KO/KF=KB/KE
=>KO*KE=KB*KF

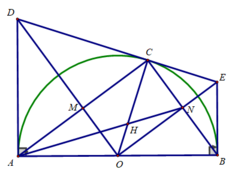
b) Xét tứ giác OMCN có:
∠(OMC) = 90 0 (AC ⊥ OD)
∠(ONC) = 90 0 (CB ⊥ OE)
∠(NCM) = 90 0 (AC ⊥ CB)
⇒ Tứ giác OMCN là hình chữ nhật
c.Cm cho: MO.ME=AM/2 .EO (hệ thức lượng) (1)
Cmtt: MO.MF=BM/2 .FO (2)
Từ (1) +(2) => EM.MO+MO.MF=AM/2.EO+BM/2.FO
=>(EM+MF).MO=(AM.EO+BM.OF)/2
=>EF.AO=(AM.EO+BM.OF)/2
=>(EF.AB)/2=(AM.EO+BM.OF)/2
=> EF.AB=AM.EO+BM.OF