Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
AM,AC là tiếp tuyến
Do đó: AM=AC và OA là tia phân giác của \(\widehat{MOC}\)
=>\(\widehat{MOC}=2\cdot\widehat{MOA}\)
Xét (O) có
BM,BD là tiếp tuyến
Do đó: BM=BD và OB là phân giác của \(\widehat{MOD}\)
=>\(\widehat{MOD}=2\cdot\widehat{MOB}\)
\(\widehat{MOC}+\widehat{MOD}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{MOA}+2\cdot\widehat{MOB}=180^0\)
=>\(2\left(\widehat{MOA}+\widehat{MOB}\right)=180^0\)
=>\(\widehat{MOA}+\widehat{MOB}=\dfrac{180^0}{2}=90^0\)
=>\(\widehat{AOB}=90^0\)
b: AB=AM+BM
mà AM=AC và BM=BD
nên AB=AC+BD
c: Xét ΔOAB vuông tại O có OM là đường cao
nên \(AM\cdot MB=OM^2\)
=>\(AC\cdot BD=R^2\) không đổi khi M di chuyển trên (O)

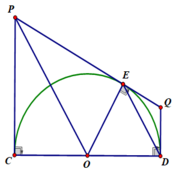
Xét tứ giác CPEO có:
∠(PCO) = ∠(PEO) = 90 0 (gt)
⇒ ∠(PCO) + ∠(PEO) = 180 0
⇒ Tứ giác CPEO là tứ giác nội tiếp
Xét tứ giác OEQD có:
∠(OEQ) = ∠(ODQ) = 90 0 (gt)
⇒ ∠(OEQ) + ∠(ODQ) = 180 0
⇒ Tứ giác OEQD là tứ giác nội tiếp

a: Xét (O) có
CE là tiếp tuyến có E là tiếp điểm
CA là tiếp tuyến có A là tiếp điểm
Do đó: CE=CA
Xét (O) có
DB là tiếp tuyến có B là tiếp điểm
DE là tiếp tuyến có E là tiếp điểm
Do đó: DB=DE
Ta có: CD=CE+ED
nên CD=CA+DB

a: Xét (O) có
CE là tiếp tuyến
CA là tiếp tuyến
Do đó: CE=CA
Xét (O) có
DE là tiếp tuyến
DB là tiếp tuyến
Do đó: DE=DB
Ta có: DE+CE=DC
nên CD=AC+BD

a: Xét (O) có
CA,CE là tiếp tuyến
nên CA=CE và OC là phân giác của góc AOE(1)
Xét (O) co
DE,DB là tiép tuyến
nên DE=DB và OD là phân giác của góc BOE(2)
CD=CE+ED
=>CD=CA+DB
b: Từ (1), (2) suy ra góc COD=1/2*180=90 độ

a: Xét (O) có
CA,CE là tiếp tuyến
nên CA=CE và OC là phân giác của góc AOE(1)
Xét (O) có
DE,DB là tiếp tuyến
nên DE=DB và OD là phân giác của góc EOB(2)
CE+ED=CD
=>CD=CA+DB
b: Từ (1), (2) suy ra góc COD=1/2*180=90 độ
c: CA=CE
OA=OE
Do đó: CO là trung trực của AE
DE=DB
OE=OB
Do đó: DO là trung trực của EB
Xét tứ giác EIOK có
góc EIO=góc EKO=góc IOK=90 độ
nên EIOK là hình chữ nhật