Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dựng tiếp tuyến với đường tròn tại B, gọi K là giao của tiếp tuyến với đường tròn tại M với tiếp tuyến với đường tròn tại B
Ta có
\(AF\perp AB;OD\perp AB;BK\perp AB\) => AF//OD//BK
\(\Rightarrow\dfrac{DE}{OA}=\dfrac{DK}{OB}\) (Talet)
Mà OA=OB
=> DE=DK (1)
Xét tg ABF có
OD//AF => \(\dfrac{DF}{OA}=\dfrac{DB}{OB}\) (Talet trong tg)
Mà OA=OB => DF=DB (2)
\(\widehat{EDF}=\widehat{KDB}\) (góc đối đỉnh)
Từ (1) (2) (3) => tg EDF = tg KDB (c.g.c)
=> EF=KB
Mà KB=KM (Hai tiếp tuyến cùng xp từ 1 điểm ngoài đường tròn thì khoảng cách từ điểm đó đến 2 tiếp điểm bằng nhau)
=> EF=KM
Ta có
EA=EM (Hai tiếp tuyến cùng xp từ 1 điểm ngoài đường tròn thì khoảng cách từ điểm đó đến 2 tiếp điểm bằng nhau)
\(\Rightarrow EA.EF=EM.KM\)
Xét tg vuông EAO và tg vuông EMO có
EO chung
EA=EM (cmt)
=> tg EAO = tg EMO (Hai tg vuông có cạnh huyền và cạnh góc vuông bằng nhau) \(\Rightarrow\widehat{EOA}=\widehat{EOM}\) (4)
C/m tương tự ta cũng có tg KMO = tg KBO \(\Rightarrow\widehat{KOB}=\widehat{KOM}\) (5)
Mà \(\widehat{EOA}+\widehat{EOM}+\widehat{KOB}+\widehat{KOM}=180^o\) (6)
Từ (4) (5) (6) \(\Rightarrow\widehat{EOM}+\widehat{KOM}=\widehat{KOE}=90^o\)
=> tg KOE là tg vuông tại O
Ta có \(OM\perp KE\) (KE là tiếp tuyến với đường tròn tại M)
Xét tg vuông KOE có
\(OM^2=KM.EM\) (Trong tg vuông bình phương đường cao từ đỉnh góc vuông xuống cạnh huyền bằng tích giữa hình chiếu 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow KM.EM=EF.EA=OM^2\) không đổi

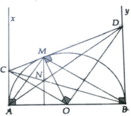
a, Từ CA, CM là tiếp tuyến của (O) chứng minh được A,C,M,O ∈ đường tròn bán kính O C 2
b, Chứng minh OC,BM cùng vuông góc với AM . từ đó suy ra OC//BM
c, S A C D B = A C + B D A B 2 = A D . A B 2
=> S A C D B nhỏ nhất khi CD có độ dài nhỏ nhất
Hay M nằm chính giữa cung AB
d, Từ tính chất hai giao tuyến => AC = CM và BM=MD, kết hợp với AC//BD
ta chứng minh được C N N B = C M M D => MN//BD => MN ⊥ AB
