Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) △ABC có M và N là trung điểm của AB, BC nên MN // AC (1)
△ACD có P và Q là trung điểm của CD, DA nên PQ // AC (2)
△SMN có I và J là trung điểm của SM, SN nên IJ // MN (3)
△SPQ có L và K là trung điểm của SQ, SP nên LK // PQ (4)
Từ (1)(2)(3)(4) suy ra IJ // LK. Do đó: I, J, K, L đồng phẳng.
Ta có: \(\dfrac{MN}{AC}=\dfrac{QP}{AC}=\dfrac{1}{2}\)
\(\dfrac{IJ}{MN}=\dfrac{LK}{PQ}=\dfrac{1}{2}\)
Từ (6)(7) suy ra: IJ = LK mà IJ // LK
Do đó: IJKL là hình bình hành.
b) Ta có: M, P lần lượt là trung điểm của AB, CD
Suy ra: MP // BC (1)
△SMP có: I, K là trung điểm của SM, SP
Suy ra: IK // MP (2)
Từ (1)(2) suy ra: IK // BC.
c) Ta có: J là điểm chung của hai mặt phẳng (IJKL) và (SBC)
Mà: IK // BC
Từ J kẻ Jx sao cho Jx // BC. Do đó, Jx là giao tuyến của hai mặt phẳng (IJKL) và (SBC).

Từ giả thiết suy ra \(\overrightarrow{PC}=-2\overrightarrow{PM}\) , \(\overrightarrow{QA}=-2\overrightarrow{QN}\) , \(\overrightarrow{BA}=2\overrightarrow{BM}\) và \(\overrightarrow{DC}=2\overrightarrow{DN}\)
Đặt \(\overrightarrow{BA}=\overrightarrow{a}\) , \(\overrightarrow{BC}=\overrightarrow{c}\) ta có \(\overrightarrow{BD}=\overrightarrow{a}+\overrightarrow{c}\) và
\(\overrightarrow{BP}=\frac{\overrightarrow{BC}-\left(-2\overrightarrow{BM}\right)}{1-\left(-2\right)}\Rightarrow3\overrightarrow{BP}=\overrightarrow{BC+}2\overrightarrow{BM}=\overrightarrow{c}+\overrightarrow{a}\)
Do đó : \(\overrightarrow{BD}=3\overrightarrow{BM}\) (1)
Hoàn toàn tương tự ta cũng được \(\overrightarrow{DB}=3\overrightarrow{DN}\) (2)
Từ (1) và (2) suy ra điều cần chứng minh

Đặt \(\frac{AB}{CD}=k\)
Do AB // CD nên \(\frac{EA}{EC}=\frac{EB}{ED}=k\) và \(\frac{FA}{FD}=\frac{FB}{FC}=k\) (như hình vẽ)
Suy ra : \(\overrightarrow{EA}=-k\overrightarrow{EC}\), \(\overrightarrow{EB}=-k\overrightarrow{ED}\) , \(\overrightarrow{FA}=-k\overrightarrow{FD}\) và \(\overrightarrow{FB}=-k\overrightarrow{FC}\)
Do M là trung điểm AB và N là trung điểm CD nên :
\(2\overrightarrow{EM}=\overrightarrow{EA}+\overrightarrow{EB}=-k\overrightarrow{EC}-k\overrightarrow{ED}=-2\left(\overrightarrow{EC}+\overrightarrow{ED}\right)=-2k\overrightarrow{EN}\)
Suy ra \(\overrightarrow{EM}=k\overrightarrow{EN}\) (1)
Hoàn toàn tương tự cũng được \(\overrightarrow{FM}=k\overrightarrow{FN}\) (2)
Từ (1) và (2) suy ra điều cần chứng minh

Từ \(2\overrightarrow{ỊJ}=\overrightarrow{AB}+\overrightarrow{CD}\) suy ra
\(AB^2+BC^2+CD^2+DA^2=AC^2+BD^2+4IJ^2\Leftrightarrow CB^2+DA^2=CA^2+DB^2+2AB^2.CD^2\)
\(\Leftrightarrow2.\overrightarrow{AB}\overrightarrow{CD}=AD^2-AC^2+BC^2-BD^2\)

Ta có:
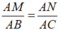
suy ra MN // BC (1) (Định lý Ta-lét đảo).
- Lại có: MN ∩ (MNI) (2)
- Từ (1) và (2) suy ra: BC // (MNI)