Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
Cho ngũ giác đều ABCDE tâm O. Chứng minh: vecto OA+OB+OC+OD+OE= vecto 0
Ta có:
\(\left(\overrightarrow{OA}+\overrightarrow{O\text{D}}\right)+\left(\overrightarrow{OB}+\overrightarrow{OE}\right)+\left(\overrightarrow{OC}+\overrightarrow{\text{OF}}\right)=\overrightarrow{0}\)

Ta có :
O là tâm => vecto AO+BO+CO+DO+EO=0(1)
Mà vecto AB+BC+CD+DE+EA=AO+OB+BO+OC+CO+OD+DO+OE+EO+OA=0(2)
Từ (1)(2)=>vecto OA+OB+OC+OD+OE=0
=>ĐPCM
hok tốt

a)
\(\begin{array}{l}\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \left( {\overrightarrow {CD} + \overrightarrow {DA} } \right)\\ = \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow {AA} = \overrightarrow 0 .\end{array}\)
b)
\(\overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {DC} \) và \(\overrightarrow {BC} - \overrightarrow {BD} = \overrightarrow {DC} \)
\( \Rightarrow \overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {BC} - \overrightarrow {BD} \)

Ta có:
\(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} \)
Mặt khác: \(\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} \)
\(\begin{array}{l} \Rightarrow 2\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} + \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} \\ \Leftrightarrow 2\overrightarrow {MN} = \left( {\overrightarrow {MA} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {DN} + \overrightarrow {CN} } \right) + \overrightarrow {BC} + \overrightarrow {AD} \\ \Leftrightarrow 2\overrightarrow {MN} = \overrightarrow 0 + \overrightarrow 0 + \overrightarrow {BC} + \overrightarrow {AD} \\ \Leftrightarrow 2\overrightarrow {MN} = \overrightarrow {BC} + \overrightarrow {AD} \end{array}\)
Lại có:
\(\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {BD} + \overrightarrow {DC} + \overrightarrow {AD} = \overrightarrow {AD} + \overrightarrow {DC} + \overrightarrow {BD} = \overrightarrow {AC} + \overrightarrow {BD} .\)
Vậy \(\overrightarrow {BC} + \overrightarrow {AD} = 2\overrightarrow {MN} = \;\overrightarrow {AC} + \overrightarrow {BD} .\)



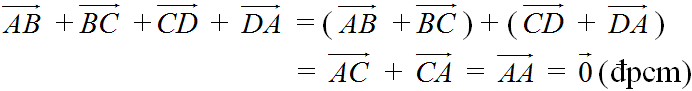
VT = \(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{AD}\).
VP = \(\overrightarrow{AE}-\overrightarrow{DE}=\overrightarrow{AE}+\overrightarrow{ED}=\overrightarrow{AD}\).
VT = VP (đpcm).