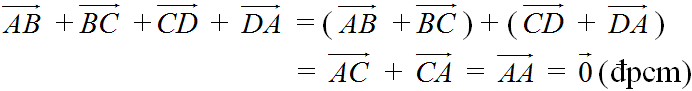Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

VT = \(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{AD}\).
VP = \(\overrightarrow{AE}-\overrightarrow{DE}=\overrightarrow{AE}+\overrightarrow{ED}=\overrightarrow{AD}\).
VT = VP (đpcm).

a) Ta có:
\(\overrightarrow{AB'}+\overrightarrow{AC'}=\overrightarrow{BC}+\overrightarrow{AB}+\overrightarrow{BC'}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}\)\(=\overrightarrow{AC}+\overrightarrow{CA}=\overrightarrow{0}\).
Vậy A là trung điểm của B'C'.
b)
A B C B' C' A'
Theo câu a ta chứng minh được A là trung điểm của B'C'.
Tương tự ta chứng minh được: B là trung điểm của A'C'; C là trung điểm của A'B'.
Từ đó suy ra ba đường thẳng AB', BB', CC' là ba đường trung tuyến của tam giác A'B'C' nên ba đường thẳng AA', BB', CC' đồng quy.

\(\begin{array}{l}A{B^2} + \overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {AB} .\overrightarrow {CA} = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {AB} .\overrightarrow {CA} \\ = \overrightarrow {AB} (\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} ) = \overrightarrow {AB} (\overrightarrow {AC} + \overrightarrow {CA} ) = \overrightarrow {AB} .\overrightarrow 0 = 0.\end{array}\)