Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích tấm đồng hình vuông ở 0 ° C là S 0 = l 0 2 . Khi bị nung nóng, kích thước của tấm đồng tăng theo mọi hướng, nên diện tích của tấm đồng này ở t ° C sẽ là :
S = l 2 = l 0 + ∆ l 2 = l 0 2 + 2 l 0 ∆ l + ∆ l 2
Theo công thức nở dài : ∆ l = ∆ l 0 ∆ t.
Vì α = 17. 10 - 6 K - 1 khá nhỏ và ∆ t = t - t 0 = t không lớn, nên ∆ l << l 0
Do đó, bỏ qua ∆ l 2 và coi gần đúng.:
S ≈ S 0 + 2 l 0 ∆ l hay ∆ S = S - S 0 ≈ 2 α S 0 ∆ t
Từ đó suy ra :
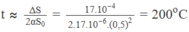

Chọn đáp án C
Khi bị nung nóng, độ dài của thanh đồng thau tăng, muốn giữ độ dài của thanh này không thay đổi, ta phải tác dụng lên hai đầu thanh một ứng suất nén sao cho độ biến dạng nén bằng độ nở dài vì nhiệt của nó
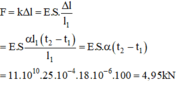

Đáp án: A
Độ tăng nhiệt độ của tấm nhôm:
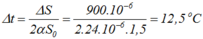
→ nhiệt độ của tấm nhôm phẳng:
t = t0 + ∆t = 12,5 o

Khi nhiệt độ tăng từ 0 ° C đến t ° C thì độ dãn dài của :
- Thanh thép : ∆ l 1 = l 01 α 1 t.
- Thanh đồng : ∆ l 2 = l 02 α 2 t.
Từ đó suy ra độ dài chênh lệch của hai thanh thép và đồng ở nhiệt độ bất kì t ° C có giá trị bằng :
∆ l = ∆ l1 – ∆ l2 = l 01 α 1 t – l 02 α 2 t = ( l 01 α 1 – l 02 α 1 )t = 50 mm
Công thức này chứng tỏ ∆ l phụ thuộc bậc nhất vào t. Rõ ràng, muốn ∆ l không phụ thuộc t, thì hệ số của t phải luôn có giá trị bằng không, tức là :
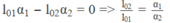
hay:
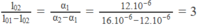
Từ đó suy ra độ dài ở 0 ° C của :
- Thanh đồng : l 02 = 3( l 01 - l 02 ) = ∆ l = 3.50 = 150 mm.
- Thanh thép : l 01 = l 02 + ∆ l = 150 + 50 = 200 mm.

1) V0 =\(\dfrac{4}{3}\pi R^3=\dfrac{4}{3}.\pi.0,05^3=\dfrac{1}{6000}\pi\)
ΔV = V0.3α.Δt = \(\dfrac{1}{6000}\pi\).3.17.10-6.100
= 2,67.10-6 (m3)
2) Thể tích thủy tinh tăng lên:
ΔV1 = V01.3α.Δt = 5.10-5.3.9.10-6.20
= 2,7.10-8
Thể tích thủy ngân tăng lên:
ΔV2 = V02.β.Δt = 5.10-5.18.10-5.20
= 1,8.10-7
Thể tích thủy ngân tràn ra ngoài:
ΔV2 - ΔV1 = 1,53.10-7 (m3)


Đáp án B