Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
+) Số tam giác được tạo từ 3 đỉnh trong 12 đỉnh: C 12 3
+) Số tam giác có 3 đỉnh là đỉnh của đa giác và 2 cạnh là cạnh của đa giác: cứ 3 đỉnh liên tiếp cho 1 tam giác thỏa mãn đề bài, nên có 12 tam giác
+) Số tam giác có 3 đỉnh là đỉnh của đa giác và 1 cạnh là cạnh của đa giác: cứ 1 cạnh, trừ đi 2 đỉnh kể, còn 8 đỉnh, với 2 đỉnh đầu mút của cạnh đó cho 1 tam giác thỏa mãn đề bài, nên có 8.12 tam giác
Vậy số tam giác có 3 đỉnh là đỉnh của đa giác và không có cạnh nào là cạnh của đa giác là C 12 3 - 12 - 12 . 8
Vậy kết quả là C 12 3 - 12 - 12 . 8 C 12 3

SỐ tam giác tạo được từ 3 đỉnh là \(C^3_{12}\)
Số tam giác có 3 đỉnh là 3 đỉnh của đa giác và 2 cạnh là cạnh của đa giác: cứ 3 đỉnh liên tiếp cho 1 tam giác thỏa mãn
=>Có 12 tam giác
Số tam giác có 3 đỉnh là đỉnh của đa giác và 1 cạnh là cạnh của đa giác
=>CÓ 8*12=96 tam giác
=>\(P=\dfrac{C^3_{12}-12-12\cdot8}{C^3_{12}}\)

Đáp án A
Phương pháp
Tìm số cạnh và số đường chéo của đa giác đều n cạnh.
Cách giải
Khi nối hai đỉnh bất kì của đa giác ta được một số đoạn thẳng, trong đó bao gồm cạnh của đa giác và đường chéo của đa giác đó.
Đa giác đều n cạnh có n đỉnh, do đó số đường chéo là C n 2 - n
Theo giả thiết bài toán ta có


Cứ hai đỉnh của đa giác ![]() đỉnh tạo thành một đoạn thẳng (bao gồm cả cạnh đa giác và đường chéo).
đỉnh tạo thành một đoạn thẳng (bao gồm cả cạnh đa giác và đường chéo).
Khi đó số đường chéo là: 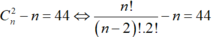
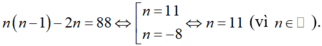
Chọn A.

Cứ hai đỉnh của đa giác n n ∈ ℕ , n ≥ 3 đỉnh tạo thành một đoạn thẳng (bao gồm cả cạnh đa giác và đường chéo).Do đó,đa giác có tất cả C n 2 đường chéo và cạnh
Đa giác n thì có n cạnh nên số đường chéo của đa giác là:
C n 2 − n = 44 ⇔ n ! n − 2 ! .2 ! − n = 44 ⇒ n ( n − 1 ) 2 − n = 44
⇔ n n − 1 − 2 n = 88 ⇔ n 2 − 3 n − 88 = 0 ⇔ n = 11 n = − 8 ⇔ n = 11 (vì n ∈ ℕ ).
Chọn đáp án A.



Đa giác đều có 15 cạnh nên có 15 đỉnh
Số đoạn thẳng nối 2 điểm bất kì (nghĩa là bao gồm tất cả các cạnh và đường chéo): \(C_{15}^2=105\)
Số đường chéo: \(105-15=90\)