Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cứ hai đỉnh của đa giác n n ∈ ℕ , n ≥ 3 đỉnh tạo thành một đoạn thẳng (bao gồm cả cạnh đa giác và đường chéo).Do đó,đa giác có tất cả C n 2 đường chéo và cạnh
Đa giác n thì có n cạnh nên số đường chéo của đa giác là:
C n 2 − n = 44 ⇔ n ! n − 2 ! .2 ! − n = 44 ⇒ n ( n − 1 ) 2 − n = 44
⇔ n n − 1 − 2 n = 88 ⇔ n 2 − 3 n − 88 = 0 ⇔ n = 11 n = − 8 ⇔ n = 11 (vì n ∈ ℕ ).
Chọn đáp án A.
Cứ đỉnh của đa giác sẽ tạo thành một đoạn thẳng (bao gồm cả cạnh đa giác và đường chéo).
Khi đó có 
cạnh.
Số đường chéo là 66-12=54.
Chọn D.
tham khảo
Đa giác đều có 20 cạnh thì sẽ có tất cả 10 đường chéo đi qua tâm của đa giác.
Một hình chữ nhật được tạo thành từ 2 đường chéo đi qua tâm, suy ra số hình chữ nhật được tạo thành là C210C102
Hình vuông được tạo thành từ 2 đường chéo vuông góc nhau, ta có tất cả 5 cặp đường chéo vuông góc nhau, suy ra có tất cả 5 hình vuông.
Vậy có 40 hình chữ nhật (không phải hình vuông) được tạo thành.
Đáp án A
Phương pháp
Tìm số cạnh và số đường chéo của đa giác đều n cạnh.
Cách giải
Khi nối hai đỉnh bất kì của đa giác ta được một số đoạn thẳng, trong đó bao gồm cạnh của đa giác và đường chéo của đa giác đó.
Đa giác đều n cạnh có n đỉnh, do đó số đường chéo là C n 2 - n
Theo giả thiết bài toán ta có
Đáp án là C
Đa giác lồi 10 cạnh thì có 10 đỉnh.
Lấy hai điểm bất kỳ trong 10 đỉnh của đa giác lồi ta được số đoạn thẳng gồm cạnh và đường chéo của đa giác lồi.
Do đó, tổng số cạnh và đường chéo của đa giác là: C 2 10
Suy ra,số đường chéo cần tìm là C 10 2 - 10 = 10 ! 8 ! . 2 ! - 10 = 35
a. Đa giác n đỉnh có \(C_n^2\) đoạn thẳng nối các đỉnh
Trong đó có n cạnh (là đường nối 2 đỉnh liền kế)
\(\Rightarrow\) Có \(C_n^2-n\) đường chéo
b. Cứ 3 đỉnh tạo thành 1 tam giác nên số tam giác là: \(C_n^3\)
c. Tam giác có 2 cạnh là 2 cạnh của tam giác khi 3 đỉnh của tam giác là 3 đỉnh liền kề
\(\Rightarrow\) có n tam giác thỏa mãn
d. Số tam giác chỉ có 1 cạnh là cạnh đa giác: có n cách chọn 2 điểm liền kề, ta có \(n-4\) cách chọn 1 điểm còn lại ko kề với 2 điểm trên
\(\Rightarrow n\left(n-4\right)\) tam giac thỏa mãn
e. Số tam giác thỏa mãn: \(C_n^3-\left(n+n\left(n-4\right)\right)\)
Đáp án D
Cứ 2 điểm k liền kề nhau sẽ tạo thành 1 đường chéo
Vậy số đường chéo là:
C
10
2
-
10
=
45
-
10
=
35
Chọn B
Gọi A là biến cố lấy ra hai đường chéo có giao điểm nằm trong đường tròn (C)
Số đường chéo của đa giác đều 20 đỉnh là
C
20
2
- 20 = 170. Khi đó, ta có số cách lấy ra 2 đường chéo trong số 170 đường là 
Để có hai đường chéo cắt nhau tại một điểm nằm trong đường tròn (C) thì hai đường chéo đó phải là đường chéo của tứ giác có 4 đỉnh là đỉnh của đa giác đều 20 đỉnh. Do đó, số cách lấy ra 2 đường chéo có giao điểm nằm trong đường tròn tâm O là C 20 4 = 4845
Vậy xác suất lấy ra hai đường chéo có giao điểm nằm trong đường tròn (C) là
Cứ hai đỉnh của đa giác
đỉnh tạo thành một đoạn thẳng (bao gồm cả cạnh đa giác và đường chéo).
Khi đó số đường chéo là: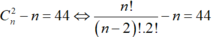
Chọn A.