Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
A. Tứ giác có ba góc vuông là hình chữ nhật → Đúng
B. Hình bình hành có một góc vông là hình chữ nhật → Đúng
C. Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình chữ nhật. → Sai
D. Tứ giác có các cạnh đối bằng nhau là hình bình hành → Đúng
Vậy chọn đáp án C

D. Hình thang có hai góc kề một đáy bằng nhau là hình bình hành.

1.
+) Tứ giác ABCD kà hình thang cân => góc ADC = BCD và AD = BC
=> tam giác ODC cân tại O => OD = OC
mà AD = BC => OA = OB
+) tam giác ODB và OCA có: OD = OC; góc DOC chung ; OB = OA
=> Tam giác ODB = OCA (c - g - c)
=> góc ODB = OCA mà góc ODC = OCD => góc ODC - ODB = OCD - OCA
=> góc EDC = ECD => tam giác EDC cân tại E => ED = EC (2)
Từ (1)(2) => OE là đường trung trực của CD
=> OE vuông góc CD mà CD // AB => OE vuông góc với AB
Tam giác OAB cân tại O có OE là đường cao nên đồng thời là đường trung trực
vậy OE là đường trung trực của AB

Đáp án cần chọn là: A
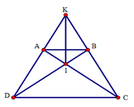
Xét tam giác ACD và tam giác BDC có:
+ AD = BC (do ABCD là hình thang cân)
+ AC = BD (do ABCD là hình thang cân)
+ CD là cạnh chung
Suy ra ΔACD = ΔBDC (c.c.c)
Suy ra A C D ^ = B D C ^ (cmt), suy ra tam giác ICD cân tại I. Do đó ID = IC (1)
Tam giác KCD có hai góc ở đáy bằng nhau nên tam giác KCD cân ở K.
Do đó KC = KD (2)
Từ (1) và (2) suy ra KI là đường trung trực của CD (*).
Xét tam giác ADB và tam giác BCA có:
+ AD = BC (cmt)
+ AB là cạnh chung
+ AC = BD
Suy ra ΔADB = ΔBCA (c.c.c)
Suy ra A B D ^ = B A C ^
Xét tam giác IAB có A B D ^ = B A C ^ nên tam giác IAB cân tại I.
Do đó IA = IB (3)
Ta có KA = KD – AD; KB = KC – BC
Mà KD = KC, AD = BC, do đó KA = KB (4)
Từ (3) và (4) suy ra KI là đường trung trực của AB. (**)
Từ (*) và (**) suy ra KI là đường trung trực của hai đáy (đpcm)