K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 8 2021
Hiểu như này:
\(\dfrac{a}{1+a}+\dfrac{b}{1+b}+\dfrac{b}{1+b}=3-\left(\dfrac{1}{1+a}+\dfrac{1}{1+b}+\dfrac{1}{1+b}\right)\le3-\dfrac{9}{1+a+1+b+1+b}=\dfrac{3\left(a+2b\right)}{3+a+2b}\)
15 tháng 12 2022
Câu 3:
Theo đề, ta có hệ:
\(\left\{{}\begin{matrix}-\dfrac{b}{2}=-2\\-\dfrac{b^2-4c}{4}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=4\\b^2-4c=-12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=4\\16-4c=-12\end{matrix}\right.\)
=>b=4 và c=7
DP
11 tháng 5 2019
Để mình nhớ xem điểm trung bình cả học sinh là 8.0 đ thì phải. Nếu 8.0 đ mà ko bị khống chế môn nào dưới 8.0đ thì đc học sinh giỏi.
30 tháng 7 2021
Em cũng bị sau đó thì tìm zalo cô giáo để gửi bài thui nè
24 tháng 9 2023
Tham khảo:
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- Tổng số giờ làm không quá 10 giờ nên \(2x + y \le 10\)
Từ đó ta có hệ bất phương trình: \(\left\{ \begin{array}{l}2x + y \le 10\\x \ge 0\\y \ge 0\end{array} \right.(x,y \in \mathbb{N})\)
Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy, ta được như hình dưới.
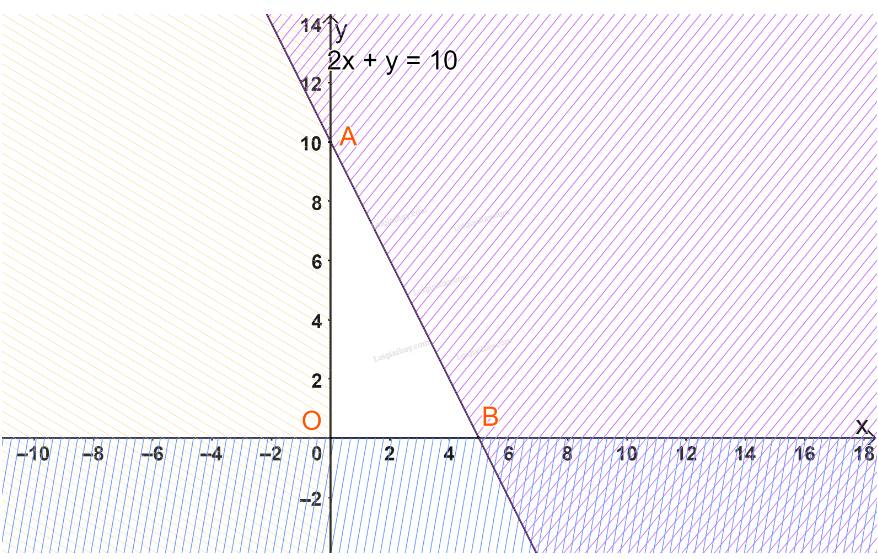
Miền không gạch chéo (miền tam giác OAB, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình.
24 tháng 6 2016
mk nghĩ các bạn bt cũng giải được bạn ko cần nói các bạn thông minh đâu
kkk
kkk