
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 20:
Ta có: \(\widehat{A}-\widehat{B}=40^0\Rightarrow\widehat{B}=\widehat{A}-40^0\)
\(\widehat{A}=2\widehat{C}\Rightarrow\widehat{C}=\frac{\widehat{A}}{2}\)
Vì AB//CD (gt) \(\Rightarrow\widehat{A}+\widehat{D}=180^0\)(hai góc trong cùng phía)\(\Rightarrow\widehat{D}=180^0-\widehat{A}\)
Tứ giác ABCD \(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\Rightarrow\widehat{A}+\left(\widehat{A}-40^0\right)+\frac{\widehat{A}}{2}+\left(180^0-\widehat{A}\right)=360^0\)
Và đến đây bạn dễ dàng tìm được góc A và từ đó suy ra được góc D.
Câu 29: Ta có:
\(\hept{\begin{cases}xy+x+y=3\\yz+y+z=8\\xz+x+z=15\end{cases}}\Leftrightarrow\hept{\begin{cases}xy+x+y+1=4\\yz+y+z+1=9\\xz+x+z+1=16\end{cases}\Leftrightarrow}\hept{\begin{cases}x\left(y+1\right)+\left(y+1\right)=4\\y\left(z+1\right)+\left(z+1\right)=9\\x\left(z+1\right)+\left(z+1\right)=16\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(x+1\right)\left(y+1\right)=4\\\left(y+1\right)\left(z+1\right)=9\\\left(z+1\right)\left(x+1\right)=16\end{cases}}\)
Đặt \(\hept{\begin{cases}x+1=a\\y+1=b\\z+1=c\end{cases}}\)với a,b,c > 1, khi đó ta có
\(\hept{\begin{cases}ab=4\\bc=9\\ca=16\end{cases}}\Leftrightarrow\hept{\begin{cases}abbc=4.9\\c=\frac{9}{b}\\ca=16\end{cases}}\Leftrightarrow\hept{\begin{cases}16b^2=36\\c=\frac{9}{b}\\a=\frac{16}{c}\end{cases}}\Leftrightarrow\hept{\begin{cases}b^2=\frac{36}{16}=\frac{9}{4}\\c=\frac{9}{b}\\a=\frac{16}{c}\end{cases}}\Leftrightarrow\hept{\begin{cases}b=\frac{3}{2}\\c=\frac{9}{\frac{3}{2}}=6\\a=\frac{16}{6}=\frac{8}{3}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=a-1=\frac{8}{3}-1=\frac{5}{3}\\y=b-1=\frac{3}{2}-1=\frac{1}{2}\\z=c-1=6-1=5\end{cases}}\)
Vậy \(P=x+y+z=\frac{5}{3}+\frac{1}{2}+5=\frac{10+3+30}{6}=\frac{43}{6}\)

Lời giải:
a.
$3x(x-1)-3x^2=-6$
$\Leftrightarrow 3x^2-3x-3x^2=-6$
$\Leftrightarrow -3x=-6$
$\Leftrightarrow x=2$
b.
$(x-7)(x+3)-(x-1)(x+4)=-3$
$\Leftrightarrow (x^2-4x-21)-(x^2+3x-4)=-3$
$\Leftrightarrow -7x-17=-3$
$\Leftrightarrow -7x=17-3=14$
$\Leftrightarrow x=14:(-7)=-2$

Xảy ra khi điều kiện đặt ra so với biến luôn đúng nên câu lệnh sẽ luôn được thực hiện
Khắc phục:thay đổi điều kiện hoặc gán lại giá trị cho biến để cho biến đủ nhỏ hoặc l

Ta có: ΔABC∼ΔDEF
nên DE/AB=EF/BC=DF/AC
=>9/6=EF/10=DF/14
=>EF/10=DF/14=3/2
=>EF=15cm; DF=21cm

i)\(\left\{{}\begin{matrix}ab=2\\a^3+b^3=9\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}ab=2\\\left(a+b\right)^3-3ab\left(a+b\right)=9\end{matrix}\right.\)
\(\Rightarrow\left(a+b\right)^3-6\left(a+b\right)-9=0\)
\(\Leftrightarrow\left(a+b\right)^3-3\left(a+b\right)^2+3\left(a+b\right)^2-9\left(a+b\right)+3\left(a+b\right)-9=0\)
\(\Leftrightarrow\left(a+b-3\right)\left[\left(a+b\right)^2+3\left(a+b\right)+3\right]=0\)
\(\Leftrightarrow a+b=3\)( \(\left(a+b\right)^2+3\left(a+b\right)+3>0;\forall a,b\)
ii) \(\left\{{}\begin{matrix}a+b+ab=23\\a^2+b^2=34\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}ab=23-\left(a+b\right)\\\left(a+b\right)^2-2ab=34\end{matrix}\right.\)
\(\Rightarrow\left(a+b\right)^2-2\left[23-\left(a+b\right)\right]=34\)
\(\Leftrightarrow\left(a+b\right)^2+2\left(a+b\right)-80=0\)
\(\Leftrightarrow\left(a+b-8\right)\left(a+b+10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b=8\\a+b=-10\end{matrix}\right.\)

a: Thay x=-4 vào B, ta được:
\(B=\dfrac{1-2\cdot\left(-4\right)}{2-\left(-4\right)}=\dfrac{1+8}{2+4}=\dfrac{9}{6}=\dfrac{3}{2}\)

Bài 2:
a: =>168x+20=6x-21
=>162x=-41
hay x=-41/162
b: \(\Leftrightarrow2\left(3x-8\right)=3\left(5-x\right)\)
=>6x-16=15-3x
=>9x=31
hay x=31/9
c: \(\Leftrightarrow4\left(x^2+8x-20\right)-\left(x+4\right)\left(x+10\right)=3\left(x^2+2x-8\right)\)
\(\Leftrightarrow4x^2+32x-80-x^2-14x-40-3x^2-6x+24=0\)
=>12x-96=0
hay x=8

\(2.8\)
Gọi 3 số tự nhiên lt là \(a-1;a;a+1\) \(\left(a\in N\text{*}\right)\)
Theo đề, có
\(a\left(a-1\right)+a\left(a+1\right)+\left(a-1\right)\left(a+1\right)=299\\ \Leftrightarrow a^2-a+a^2+a+a^2-1=299\\ \Leftrightarrow3a^2=300\\ \Leftrightarrow a^2=100\Leftrightarrow a=10\left(a\in N\text{*}\right)\)
Vậy 3 số đó là 99;100;101
\(2.1\\ a,A=x^3-2x^2+4x^2-8x-2x+4-x^3-x\\ A=2x^2-11x+4\\ b,x=-2\\ \Leftrightarrow A=2\cdot4+22+4=34\\ c,A=4\Leftrightarrow2x^2-11x+4=4\\ \Leftrightarrow x\left(2x-11\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{11}{2}\end{matrix}\right.\\ d,A>-21\\ \Leftrightarrow2x^2-11x+4+21>0\\ \Leftrightarrow2x^2-11x+25>0\\ \Leftrightarrow2\left(x^2-2\cdot\dfrac{11}{4}x+\dfrac{121}{16}-\dfrac{121}{16}+25\right)>0\\ \Leftrightarrow2\left(x-\dfrac{11}{4}\right)^2+\dfrac{279}{8}>0\left(luôn.đúng\right)\\ \Leftrightarrow x\in R\)
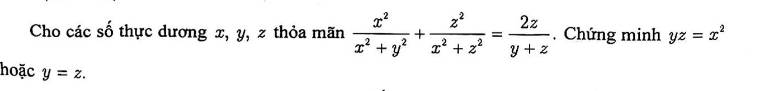 cho mình hởi bài này làm thế nào ạ
cho mình hởi bài này làm thế nào ạ

 Giúp mình làm bài này với ạ
Giúp mình làm bài này với ạ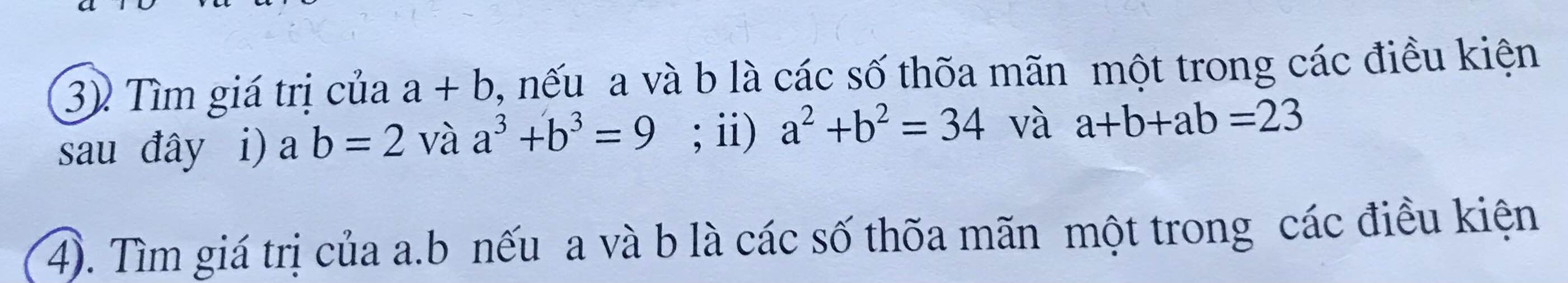

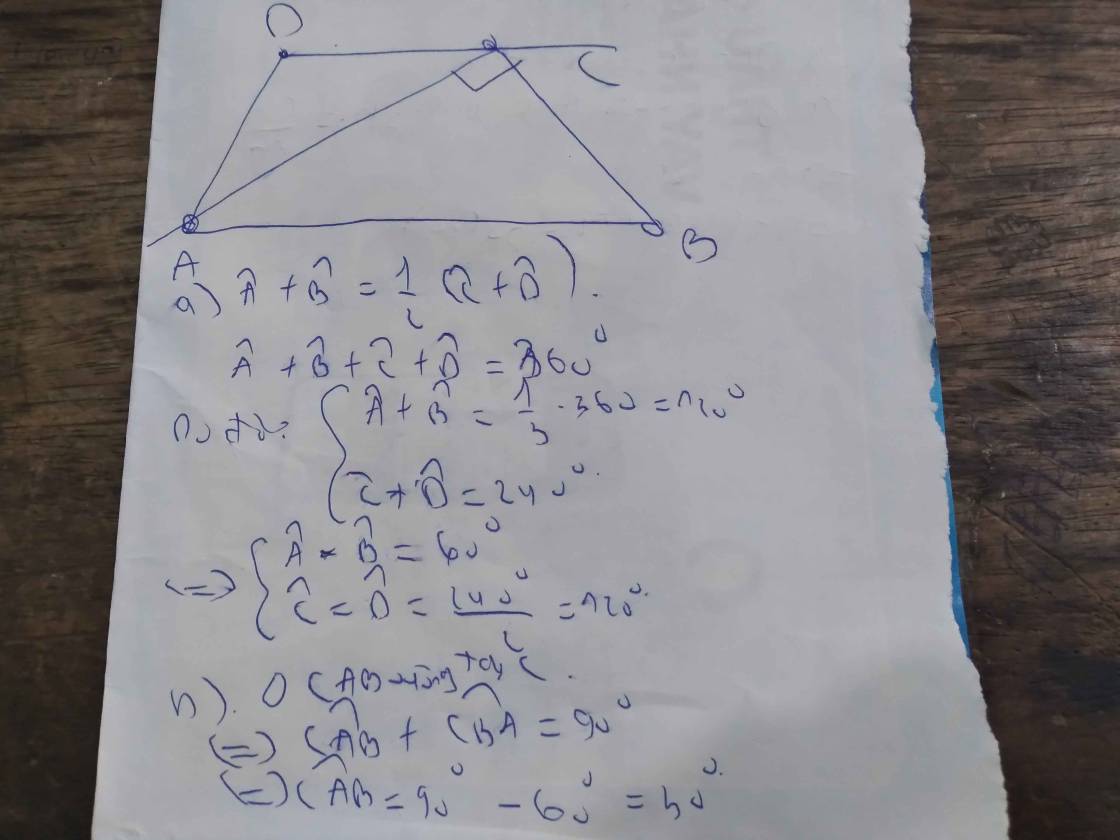



 Bạn nào làm bài này cho mình được không ngày mai phải nộp rồi
Bạn nào làm bài này cho mình được không ngày mai phải nộp rồi
Lời giải:
$\frac{x^2}{x^2+y^2}+\frac{z^2}{x^2+z^2}=\frac{2z}{y+z}$
$\Leftrightarrow \frac{x^4+2x^2z^2+y^2z^2}{(x^2+y^2)(x^2+z^2)}=\frac{2z}{y+z}$
$\Leftrightarrow (x^4+2x^2z^2+y^2z^2)(y+z)=2z(x^4+x^2z^2+x^2y^2+y^2z^2)$
$\Leftrightarrow x^4y-x^4z+2x^2yz^2-2x^2y^2z+y^3z^2-y^2z^3=0$
$\Leftrightarrow x^4(y-z)-2x^2yz(y-z)+y^2z^2(y-z)=0$
$\Leftrightarrow (y-z)(x^4-2x^2yz+y^2z^2)=0$
$\Leftrightarrow (y-z)(x^2-yz)^2=0$
$\Leftrightarrow y-z=0$ hoặc $x^2-yz=0$
$\Leftrightarrow y=z$ hoặc $x^2=yz$