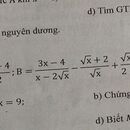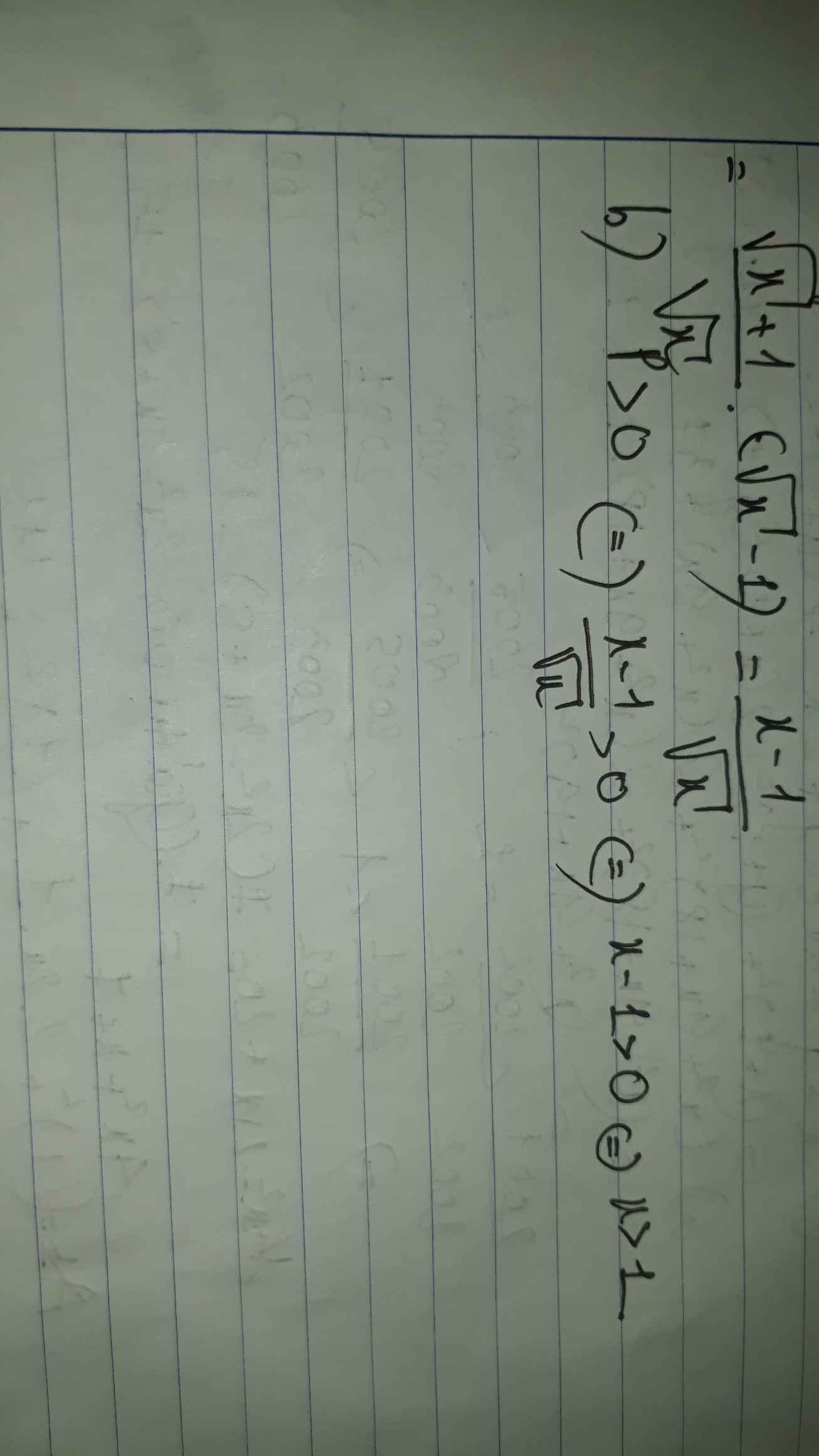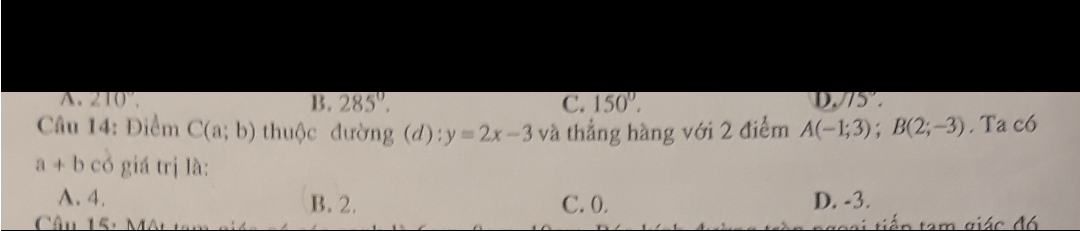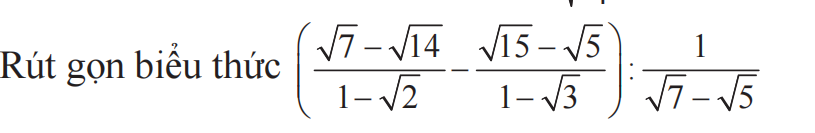Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a,mấy đoạn dấu : dấu+ trong đề hơi khó nhìn
\(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\)
\(P=\left[\dfrac{\sqrt{x}.\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right]:\left(\dfrac{\sqrt{x}-1+2}{x-1}\right)\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{x-1}=\dfrac{\sqrt{x}+1}{\sqrt{x}}:\dfrac{1}{\sqrt{x}-1}=\dfrac{x-1}{\sqrt{x}}\)
b, \(P>0=>\dfrac{x-1}{\sqrt{x}}>0=>x-1>0< =>x>1\)(tm)
Vậy \(x>1\) .....
\(\)

=\(\left(3\sqrt{3}-3\sqrt{3}+2\sqrt{6}\right):3\sqrt{3}\)
\(=1-\dfrac{\sqrt{6}}{2}+\dfrac{2\sqrt{2}}{3}\)
=\(\dfrac{6}{6}-\dfrac{3\sqrt{6}}{6}+\dfrac{4\sqrt{2}}{6}\)
=\(\dfrac{6+\sqrt{6}}{6}\)

10:
Độ dài bán kính là;
\(\sqrt{\dfrac{78.5}{3,14}}=5\left(m\right)\)
Chu vi là: 5*2*3,14=31,4(m)

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>\(\widehat{AMB}=90^0\)
b: Xét ΔOMC vuông tại M có MH là đường cao
nên \(HC\cdot HO=HM^2\left(1\right)\)
Xét ΔMAB vuông tại M có MH là đường cao
nên \(HA\cdot HB=HM^2\left(2\right)\)
Từ (1) và (2) suy ra \(HC\cdot HO=HA\cdot HB\)
c: Xét tứ giác AMBQ có
O là trung điểm của AB và MQ
Do đó: AMBQ là hình bình hành
Hình bình hành AMBQ có AB=MQ
nên AMBQ là hình bình hành

Gọi số khẩu trang ngày 1 may được của tổ 1 và tổ 2 lần lượt là x,y
Theo đề, ta có: x+y=50000 và 1,15x+1,12y=56900
=>x=30000 và y=20000
=>tổ 1 may được 2,15*30000=64500cái và tổ 2 may được 2,12*20000=42400 cái

Gọi phương trình đường thẳng đi qua 2 điểm \(A,B\) là \(y=mx+n\)
Do \(\left\{{}\begin{matrix}A\in AB\\B\in AB\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3=-m+n\\-3=2m+n\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=-2\\n=1\end{matrix}\right.\)
\(\Rightarrow AB:y=-2x+1\)
Do \(C\left(a,b\right)\in\left(d\right):y=2x-3\Rightarrow b=2a-3\) (1)
Mặt khác, để \(A,B,C\) thẳng hàng thì \(C\in AB\Rightarrow b=-2a+1\) (2)
Từ (1) và (2) ta có \(a=1,b=-1\) nên \(a+b=0\)
Do C thuộc d nên: \(b=2a-3\) \(\Rightarrow C\left(a;2a-3\right)\)
Gọi phương trình đường thẳng d1 qua 2 điểm A; B có dạng:
\(y=mx+n\)
A; B thuộc d1 nên: \(\left\{{}\begin{matrix}3=-m+n\\-3=2m+n\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m=-2\\n=1\end{matrix}\right.\)
\(\Rightarrow\) Phương trình d1: \(y=-2x+1\)
A;B;C thẳng hàng khi và chỉ khi C thuộc d1
\(\Rightarrow2a-3=-2a+1\)
\(\Rightarrow4a=4\Rightarrow a=1\Rightarrow b=-1\)
\(\Rightarrow a+b=0\)

20.
Đặt \(\left(x;y;z\right)=\left(a^3;b^3;c^3\right)\Rightarrow abc=1\)
\(a^3+b^3=\left(a+b\right)\left(a^2+b^2-ab\right)\ge\left(a+b\right)\left(2ab-ab\right)=ab\left(a+b\right)\)
\(\Rightarrow P=\sum\dfrac{1}{a^3+b^3+1}\le\sum\dfrac{1}{ab\left(a+b\right)+1}=\sum\dfrac{abc}{ab\left(a+b\right)+abc}=\sum\dfrac{c}{a+b+c}=1\)
21.
Đề bài sai, biểu thức này ko tồn tại min hay max (nó chỉ tồn tại khi x;y;z là số thực không âm. Khi đó min P xảy ra tại \(\left(x;y;z\right)=\left(\dfrac{1}{2};\dfrac{1}{2};0\right)\) và hoán vị)
22.
Đề bài sai, biểu thức không tồn tại min. Nó chỉ tồn tại khi có thêm điều kiện x;y;z là độ dài 3 cạnh của 1 tam giác (em cứ thay giá trị \(x=2;y=1.9999;z=8.0001\) vào tính giá trị P sẽ hiểu tại sao đề sai)

\(=\left[\dfrac{\sqrt{7}\left(1-\sqrt{2}\right)}{1-\sqrt{2}}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\right]\cdot\left(\sqrt{7}-\sqrt{5}\right)\\ =\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)=7-5=2\)