Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương trình đường thẳng IH
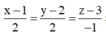
![]()
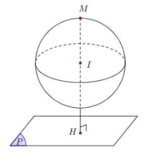
Độ dài MH lớn nhất => M là một trong hai giao điểm của MI và (S)
Suy ra MI ≡ MH, gọi M(1+2t;2+2t;3-t) ∈ (S)
![]()
Do đó
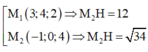
![]()

Gọi mặt phẳng là (P) dễ kí hiệu
\(d\left(M;\left(P\right)\right)=\frac{\left|-6+2+2-7\right|}{\sqrt{2^2+2^2+1}}=\frac{9}{3}=3\)
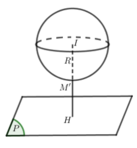
Áp dụng định lý Pitago:
\(R=\sqrt{3^2+4^2}=5\)
Phương trình mặt cầu:
\(\left(x+3\right)^2+\left(y-1\right)^2+\left(z-2\right)^2=25\)
\(\Leftrightarrow x^2+y^2+z^2+6x-2y-4z-11=0\)

Mặt (S) cầu có tâm I (1;2;3), R=3.
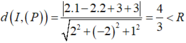 mặt phẳng cắt mặt cầu theo một đường tròn
mặt phẳng cắt mặt cầu theo một đường tròn
Gọi M (a;b;c) là điểm trên mặt cầu sao cho khoảng cách từ M đến (P) lớn nhất.
Khi M thuộc đường thẳng Δ vuông đi qua M và vuông góc với (P)
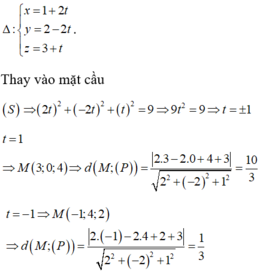
Vậy M (3;0;4) a + b + c = 7.
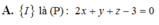
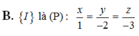
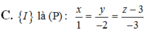
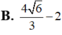

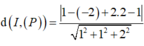



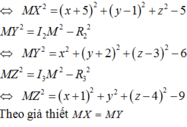



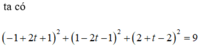
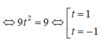
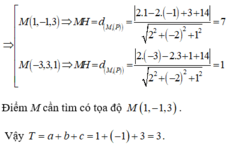
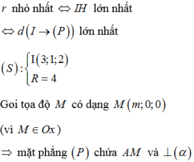

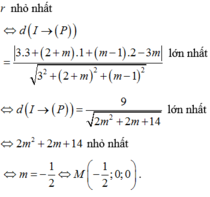

Chọn đáp án C