Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*) Từ hai biểu thức dòng điện, rút ra 2 kết luận sau: khi \(\omega\) thay đổi thì
+) I cực đại tăng \(\frac{I_2}{I_1}=\sqrt{\frac{3}{2}}\Rightarrow \frac{Z_1}{Z_2}=\sqrt{\frac{3}{2}}\)
+) Pha ban đầu của i giảm 1 góc bằng: \(\frac{\pi}{3}-\left(-\frac{\pi}{12}\right)=\frac{5\pi}{12}=75^0\)
tức là hai véc tơ biểu diễn Z1 và Z2 lệch nhau 75 độ, trong đó Z2 ở vị trí cao hơn
*) Dựng giản đồ véc-tơ:
Trong đó: \(\widehat{AOB}=75^0\);
Đặt ngay: \(Z_1=OB=\sqrt{\frac{3}{2}}\Rightarrow Z_2=1\)
Xét tam giác OAB có \(\widehat{AOB}=75^0;OA=1;OB=\sqrt{\frac{3}{2}}\) và đường cao OH.
Với trình độ của bạn thì thừa sức tính ngay được: \(OH=\frac{\sqrt{3}}{2}\)
\(\Rightarrow R=OH=\frac{\sqrt{3}}{2}\)
*) Tính \(Z_L,Z_C\):
\(Z_1^2=R^2+\left(Z_L-Z_C\right)^2;\left(Z_L< Z_C\right)\)
\(Z_2^2=R^2+\left(\sqrt{3}Z_L-\frac{Z_C}{\sqrt{3}}\right)^2\)
Thay số vào rồi giải hệ 2 ẩn bậc nhất, tìm được: \(Z_L=\frac{\sqrt{3}}{2};Z_C=\sqrt{3}\)
*) Tính
\(\frac{R^2L}{C}=\frac{R^2\cdot\left(L\omega_1\right)}{C\omega_1}=R^2Z_LZ_C\\ =\left(\frac{\sqrt{3}}{2}\right)^2\cdot\frac{\sqrt{3}}{2}\cdot\sqrt{3}=\frac{9}{4}\)
Ra $\frac{1}{2}$ ông ạ
Thầy tôi bảo có cách dùng giản đồ vector ngắn kinh khủng mà chưa ngộ ra.

khi w=wo trong mạch xảy ra cộng hưởng ,cường độ dòng điện hiêu dụng là I max,còn khi w=w1 hoặc w=w2 thì dòng điện trong mạch có cùng giá trị hiệu dụng
nên \(\omega_0^2=\omega_1\omega_2=\frac{1}{LC}\Rightarrow\omega_2L=\frac{1}{\omega_1C}\Rightarrow Z_{L2}=Z_{C1}\)
\(I_{max}=\frac{U}{R}\)
\(I=\frac{U}{\sqrt{R^2+\left(Z_{L1}-Z_{C1}\right)^2}}=\frac{U}{\sqrt{R^2+\left(Z_{L1}-Z_{L2}\right)^2}}\)
Theo giả thiết: \(I=\frac{I_{max}}{\sqrt{5}}\)
\(\Rightarrow\frac{U}{\sqrt{R^2+\left(Z_{L1}-Z_{L2}\right)^2}}=\frac{U}{\sqrt{5}R}\Rightarrow R^2+\left(Z_{L1}-Z_{L2}\right)^2=5R^2\)
\(\Rightarrow\left|Z_{L1}-Z_{L2}\right|=2R\)
\(\Rightarrow L\left(\omega_2-\omega_1\right)=2R\Rightarrow\frac{1}{\pi}.150\pi=2R\Rightarrow R=75\Omega\)
Đáp án B.

\(\varphi=\varphi_u-\varphi_i=0-\left(-\frac{\pi}{4}\right)=\frac{\pi}{4}\)
\(\tan\varphi=\frac{Z_L-Z_C}{R}=1\Rightarrow Z_L-Z_C=R\)
\(\Rightarrow Z=\sqrt{R^2+\left(Z_L-Z_C\right)^2}=R\sqrt{2}\)
Mà \(Z=\frac{U}{I}=\frac{200}{2}=100\Rightarrow R=\frac{100}{\sqrt{2}}=50\sqrt{2}\)

Giải thích: Đáp án B
+ Khi L = L1 và ω = 120π rad/s thì UL có giá trị cực đại nên sử dụng hệ quả khi UL max ta có:
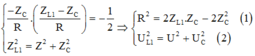
Thay U = 120 V và UC = 40 3 V ta có:
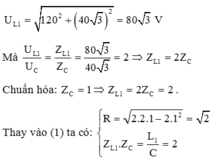
+ Khi L2 = 2L1 thì vẫn thay đổi ω để UL max nên:


\(Z_C=\frac{1}{\omega C}=100\Omega\)
L thay đổi để \(U_{Lmax}\) khi \(Z_L=\frac{R^2+Z_C^2}{Z_C}=200\Omega\)
\(\Rightarrow L=\frac{Z_L}{\omega}=\frac{2}{\pi}\)(H)
