Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(R_{tđ}=\dfrac{\left(R_1+R_2\right)R_3}{R_1+R_2+R_3}=\dfrac{\left(R+R\right)R}{R+R+R}=\dfrac{2R^2}{3R}=\dfrac{2}{3}R\)

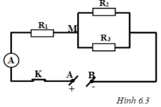
a) \(R_{tđ}=\dfrac{R_{23}.R_1}{R_{23}+R_1}=\dfrac{\left(R_2+R_3\right).R_1}{\left(R_2+R_3\right)+R_1}=\dfrac{\left(6+4\right).2}{\left(6+4\right)+2}=\dfrac{5}{3}\left(\Omega\right)\)
b) \(R_{tđ}=R_1+R_{23}=R_1+\dfrac{R_2.R_3}{R_2+R_3}=2+\dfrac{6.4}{6+4}=\dfrac{22}{5}\left(\Omega\right)\)
Câu a:
\(R_{23}=R_2+R_3=6+4=10\Omega\)
\(R_{tđ}=\dfrac{R_{23}\cdot R_1}{R_{23}+R_1}=\dfrac{10\cdot2}{10+2}=\dfrac{5}{3}\Omega\)
Câu b:
\(R_{23}=\dfrac{R_2\cdot R_3}{R_2+R_3}=\dfrac{6\cdot4}{6+4}=2,4\Omega\)
\(R_{tđ}=R_1+R_{23}=2+2,4=4,4\Omega\)

Cho ba điện trở R1 = R2 = R3 = R mắc song song với nhau. Điện trở tương đương đương Rtđ của đoạn mạch đó có thể nhận giá trị nào trong các giá trị
A. Rtđ = R.
B. Rtđ = 2R.
C. Rtđ = 3R.
D. Rtđ = R/3
Giải thích:
\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}=\dfrac{1}{R}+\dfrac{1}{R}+\dfrac{1}{R}=\dfrac{3}{R}\)
\(\Rightarrow R_{tđ}=\dfrac{R}{3}\Omega\)
Chọn D.

\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}=\dfrac{1}{R}+\dfrac{1}{R}+\dfrac{1}{R}=\dfrac{3}{R}\\ \Rightarrow R_{tđ}=\dfrac{R}{3}\)
Đề chưa rõ lắm nhé, bạn dựa vào để tính ...

Vì R 3 song song với R 1 và R 2 nên:
U = U 1 = U 2 = U 3 = 4,8V
I = I 1 + I 2 + I 3 → I 3 = I - I 1 - I 2 = 1,5 – 0,8 – 0,4 = 0,3A
Điện trở
R
3
bằng: 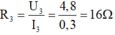
Điện trở tương đương của toàn mạch là: 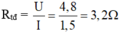

Chọn C
Do điện trở R 2 nối tiếp với điện trở R 3 nên ta có: R 23 = R 2 + R 3 = r + 6r = 7r
Điện trở tương đương của đoạn mạch này là:
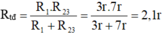

Cách 1:
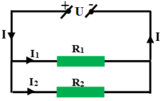
a) Nhận xét: Đoạn mạch gồm hai đoạn mạch con AM (chỉ gồm R1) ghép nối tiếp với MB ( gồm R2 // với R1).
Điện trở tương đương của đoạn mạch là:
Rtđ = RAM + RMB =
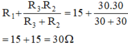
b)
Cường độ dòng điện qua điện trở R1 chính là cường độ dòng điện qua mạch chính:
I1 = I = UAB /Rtđ = 12/30 = 0,4A
Hiệu điện thế giữa hai đầu dây điện trở R1 là: U1 = R1.I1 = 15.0,4 = 6 V.
Hiệu điện thế giữa hai đầu dây điện trở R2 và R3 là:
U2 = U3 = UMB = UAB – UAM = 12 – 6 = 6V
Vì R2 = R3 nên cường độ dòng điện qua R2 và R3 là: I2 = I3 = U3/R3 = 6/30 = 0,2A
Cách 2: Áp dụng cho câu b (có sử dụng kết quả câu a)
Vì R1 ghép nối tiếp với đoạn mạch RAM nên ta có:
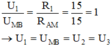
(vì MB chứa R2 //R3 nên UMB = U2 = U3).
Mà U1 + UMB = UAB → U1 = UMB = U2 = U3 = UAB /2 = 12/2 =6 V
→ Cường độ dòng điện qua các điện trở là:
I1 = U1/R1 = 6/15 = 0,4A; I2 = U2/R2 = 6/30 = 0,2A;
I3 = U3/R3 = 6/30 = 0,2A;
(hoặc I3 = I1 –I2 = 0,4 – 0,2 = 0,2 A)
ta có :
\(R_{t\text{đ}}=\left(\dfrac{R_2\cdot R_3}{R_2+R_3}\right)+R_1\)
\(=\dfrac{R^2}{2R}+R\) =\(=\dfrac{R^2}{2R}+\dfrac{2R^2}{2R}\)=\(\dfrac{3R^2}{2R}\)
Từ đề bài ta có :
\(\dfrac{3R^2}{2R}=120\)
Giải phương trình được:
R = 80Ω
Bài làm:
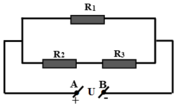
Sơ đồ mạch điện là: \(\left(R_2\text{/}\text{/}R_3\right)ntR_1\)
Từ sơ đồ mạch điện nên: \(\Rightarrow R_{23}=\dfrac{R_2\cdot R_3}{R_2+R_3}=\dfrac{R^2}{2R}=\dfrac{R}{2}\left(\Omega\right)\)
\(\Rightarrow R_{TĐ}=R_{23}+R_1=\dfrac{R}{2}+R\left(\Omega\right)\)
Mà: \(R_{TĐ}=120\left(\Omega\right)\)
\(\Rightarrow\dfrac{R}{2}+R=120\Rightarrow R=80\left(\Omega\right)\)
Vậy ...................................