PN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PN
6
1 tháng 10 2021
\(M=2+2^2+...+2^{60}\)
\(=2\left(1+2\right)+...+2^{59}\left(1+2\right)\)
\(=3\cdot\left(2+...+2^{59}\right)⋮3\)
\(M=2+2^2+...+2^{60}\)
\(=2\left(1+2+2^2\right)+...+2^{58}\left(1+2+2^2\right)\)
\(=7\cdot\left(2+...+2^{58}\right)⋮7\)
PT
1
PT
1
CM
24 tháng 4 2019
Sơ đồ con đường |
Lời giải chi tiết |
|
Ta có: C = 2 + 2 2 + 2 3 + 2 4 + ... + 2 59 + 2 60 = 2 1 + 2 + 2 3 1 + 2 + ... + 2 59 1 + 2 = 2.3 + 2 3 .3 + ... + 2 59 .3 = 2 + 2 3 + ... + 2 59 .3 ⇒ C ⋮ 3 |
PT
1
CM
14 tháng 5 2019
Sơ đồ con đường |
Lời giải chi tiết |
Bước 1. Phân tích sao cho tổng đó thành tích các thừa số trong đó có một thừa số chia hết cho 7. Bước 2. Áp dụng tính chất chia hết của một tích. |
Ta có: A = 2 + 2 2 + 2 3 + … + 2 60 = 2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + … + 2 58 + 2 59 + 2 60 = 2. 1 + 2 + 2 2 + 2 4 . 1 + 2 + 2 2 + … + 2 58 . 1 + 2 + 2 2 = 2. 1 + 2 + 2 2 + 2 4 . 1 + 2 + 2 2 + … + 2 58 . 1 + 2 + 2 2 = 2 + 2 4 + … + 2 58 .7 ⇒ A ⋮ 7 |
PT
1
PT
1
10 tháng 10 2021
\(B=2+2^2+2^3+...+2^{60}\)
\(=2\left(1+2+2^2\right)+...+2^{58}\left(1+2+2^2\right)\)
\(=7\cdot\left(2+...+2^{58}\right)⋮7\)
VN
1
VN
Võ Ngọc Phương
VIP
2 tháng 11 2023
Sửa dùm mình dòng cuối cùng là " Vậy \(A⋮5\) " nha. Cảm ơn bạn.
SX
1
28 tháng 2 2022
Đề sai, viết lại thành:
A= 21+22+23+24+...+259+260
Giải:
A=21+22+23+...............+259+260
A=(21+22+23)+...............+(258+259+260)
A=2.(1+2+22)+............+258.(1+2+22)
A=2.7+.......................+258.7
A=(2+24+..............+258).7 ⋮ 7(đpcm)
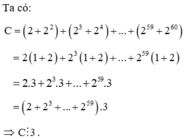
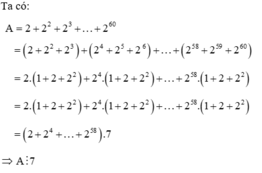
Lời giải:
$M=4+4+2^3+...+2^{60}$
$=8+(2^3+2^4)+(2^5+2^6)+...+(2^{59}+2^{60})$
$=8+2^3(1+2)+2^5(1+2)+...+2^{59}(1+2)$
$=8+2^3.3+2^5.3+....+2^{59}.3$
$=8+3(2^3+2^5+...+2^{59})$
Vì $3(2^3+2^5+...+2^{59})\vdots 3$ mà $8\not\vdots 3$ nên $M\not\vdots 3$
Bạn xem lại đề.
nhưng đề có gì ai ư