Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a^2=b+4010\Rightarrow\left(x+y+z\right)^2=x^2+y^2+z^2+4010\Rightarrow x^2+y^2+z^2+2xy+2yz+2xz=x^2+y^2+z^2+4010\)
\(\Rightarrow2xy+2yz+2xz=4010\Rightarrow xy+yz+xz=2005\)
\(x\sqrt{\frac{\left(2015+y^2\right)\left(2005+z^2\right)}{\left(2005+x^2\right)}}=x\sqrt{\frac{\left(xz+yz+xy+y^2\right)\left(xy+xz+yz+z^2\right)}{\left(xy+yz+x^2+xz\right)}}\)
\(=x\sqrt{\frac{\left(z\left(x+y\right)+y\left(x+y\right)\right)\left(x\left(y+z\right)+z\left(y+z\right)\right)}{\left(y\left(x+z\right)+x\left(x+z\right)\right)}}=x\sqrt{\frac{\left(y+z\right)^2\left(x+y\right)\left(y+z\right)}{\left(x+y\right)\left(x+z\right)}}\)
\(=x\sqrt{\left(y+z\right)^2}=x\left(y+z\right)=xy+xz\)
tương tự : \(y\sqrt{\frac{\left(2015+x^2\right)\left(2015+z^2\right)}{2015+y^2}}=xy+yz;z\sqrt{\frac{\left(2005+x^2\right)\left(2005+y^2\right)}{2015+z^2}}=xz+yz\)
\(\Rightarrow M=xy+xz+xy+yz+xz+yz=2\left(xy+yz+xz\right)=2\cdot2005=4010\)

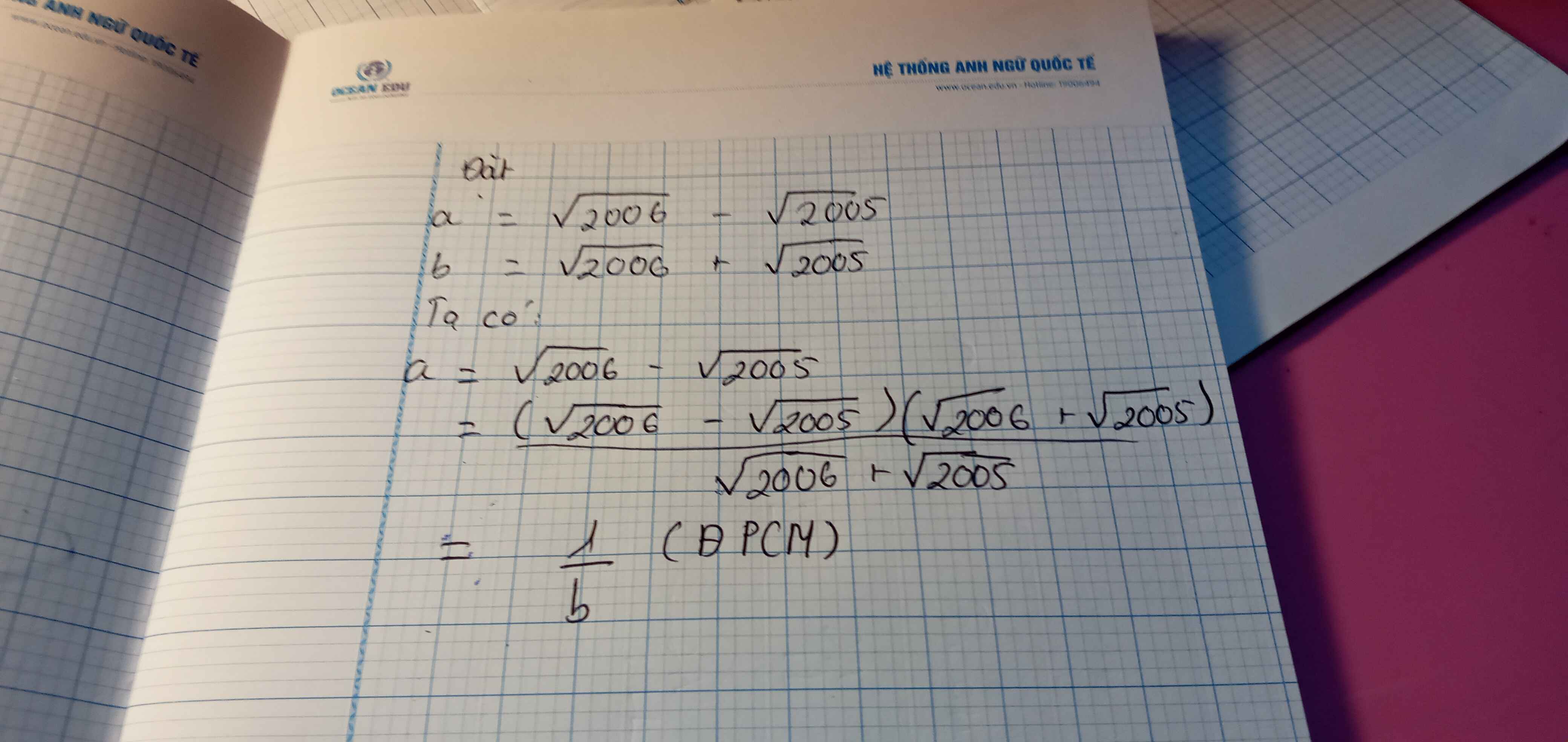
Đặt \(a=\sqrt{2006}-\sqrt{2005};b=\sqrt{2006}+\sqrt{2005}\)
Ta có
\(a=\sqrt{2006}-\sqrt{2005}=\dfrac{\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)}{\sqrt{2006}+\sqrt{2005}}=\dfrac{1}{b}\)
\(\RightarrowĐfcm\)

ĐKXĐ: ...
\(\Leftrightarrow2\sqrt{x-5}+2\sqrt{y-2005}+2\sqrt{z+2007}=x+y+z\)
\(\Leftrightarrow x-5-2\sqrt{x-5}+1+y-2005-2\sqrt{y-2005}+1+z+2007-2\sqrt{z-2007}+1=0\)
\(\Leftrightarrow\left(\sqrt{x-5}-1\right)^2+\left(\sqrt{y-2005}-1\right)^2+\left(\sqrt{z+2007}-1\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x-5}-1=0\\\sqrt{y-2005}-1=0\\\sqrt{z+2007}-1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=6\\y=2006\\z=-2006\end{matrix}\right.\)

Điều kiện \(x^2-1\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}x\le-1\\x\ge1\end{matrix}\right.\)
Đặt \(x-\sqrt{x^2-1}=a\) thì ta có pt trở thành:
\(\left(1+a\right)^{2005}+\left(1+\dfrac{1}{a}\right)^{2005}=2^{2006}\)
Ta có:
\(\left(1+a\right)^{2005}+\left(1+\dfrac{1}{a}\right)^{2005}\ge2^{2005}\left(\sqrt{a^{2005}}+\dfrac{1}{\sqrt{a^{2005}}}\right)\ge2^{2006}\)
Đấu = xảy ra khi a = 1 hay
\(x-\sqrt{x^2-1}=1\)
\(\Leftrightarrow x=1\)

\(y=\frac{1}{9+4\sqrt{5}}=\frac{1}{\left(\sqrt{5}+2\right)^2}\)
\(\Rightarrow N=\frac{1}{\left(\sqrt{5}-2\right)^2}-\frac{3}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}+\frac{2}{9+4\sqrt{5}}\)
\(=\frac{1}{9-4\sqrt{5}}+\frac{2}{9+4\sqrt{5}}-3=\frac{9+4\sqrt{5}+18-8\sqrt{5}}{\left(9-4\sqrt{5}\right)\left(9+4\sqrt{5}\right)}-3=24-4\sqrt{5}\)
\(S^2=x^2\left(1+y^2\right)+y^2\left(1+x^2\right)+2xy\sqrt{\left(1+x^2\right)\left(1+y^2\right)}\)
\(=x^2+y^2+x^2y^2+1+x^2y^2-1+2xy\sqrt{\left(1+x^2\right)\left(1+y^2\right)}\)
\(=\left(1+x^2\right)\left(1+y^2\right)+2xy\sqrt{\left(1+x^2\right)\left(1+y^2\right)}+x^2y^2-1\)
\(=\left(xy+\sqrt{\left(1+x^2\right)\left(1+y^2\right)}\right)^2-1\)
\(=2005^2-1\)
\(\Rightarrow S=\pm\sqrt{2005^2-1}\)
c/
Giả sử \(\sqrt[3]{3+\sqrt[3]{3}}+\sqrt[3]{3-\sqrt[3]{3}}< 2\sqrt[3]{3}\)
\(\Leftrightarrow\sqrt[3]{3+\sqrt[3]{3}}-\sqrt[3]{3}< \sqrt[3]{3}-\sqrt[3]{3-\sqrt[3]{3}}\)
\(\Leftrightarrow\frac{\sqrt[3]{3}}{\sqrt[3]{\left(3+\sqrt[3]{3}\right)^2}+\sqrt[3]{9+3\sqrt[3]{3}}+\sqrt[3]{9}}< \frac{\sqrt[3]{3}}{\sqrt[3]{9}+\sqrt[3]{9-3\sqrt[3]{3}}+\sqrt[3]{\left(3-\sqrt[3]{3}\right)^2}}\)
\(\Leftrightarrow\sqrt[3]{\left(3+\sqrt[3]{3}\right)^2}+\sqrt[3]{9+3\sqrt[3]{3}}+\sqrt[3]{9}>\sqrt[3]{9}+\sqrt[3]{9-3\sqrt[3]{3}}+\sqrt[3]{\left(3-\sqrt[3]{3}\right)^2}\)
\(\Leftrightarrow\sqrt[3]{\left(3+\sqrt[3]{3}\right)^2}+\sqrt[3]{9+3\sqrt[3]{3}}>\sqrt[3]{9-3\sqrt[3]{3}}+\sqrt[3]{\left(3-\sqrt[3]{3}\right)^2}\) (1)
Ta có: \(\left\{{}\begin{matrix}\sqrt[3]{9+3\sqrt[3]{3}}>\sqrt[3]{9-3\sqrt[3]{3}}\\\sqrt[3]{\left(3+\sqrt[3]{3}\right)^2}>\sqrt[3]{\left(3-\sqrt[3]{3}\right)^2}\end{matrix}\right.\)
Nên (1) đúng
Vậy BĐT ban đầu đúng

\(x-\sqrt{x^2-1}=\frac{x^2-\left(x^2-1\right)}{x+\sqrt{x^2-1}}=\frac{1}{x+\sqrt{x^2-1}}=t\)\(\Rightarrow x+\sqrt{x^2-1}=\frac{1}{t}\)
Ta có: \(\left(1+t\right)^{2015}+\left(1+\frac{1}{t}\right)^{2015}=2^{2016}\)(1)
Áp dụng Côsi ta có:
\(1+t\ge2\sqrt{t}\Rightarrow\left(1+t\right)^{2015}\ge2^{2015}.\sqrt{t^{2015}}\)
\(1+\frac{1}{t}\ge\frac{2}{\sqrt{t}}\Rightarrow\left(1+\frac{1}{t}\right)^{2015}\ge\frac{2^{2015}}{\sqrt{t^{2015}}}\)
\(\Rightarrow\left(1+t\right)^{2015}+\left(1+\frac{1}{t}\right)^{2015}\ge2^{2015}\left(\sqrt{t^{2015}}+\frac{1}{\sqrt{t^{2015}}}\right)\)
\(\ge2^{2015}.2\sqrt{\sqrt{t^{2015}}.\frac{1}{\sqrt{t^{2015}}}}=2^{2016}\)
Dấu "=" xảy ra khi và chỉ khi t = 1.
Do đó, từ (1) => \(t=\frac{1}{x+\sqrt{x^2-1}}=1\Rightarrow x+\sqrt{x^2-1}=1\)
\(\Rightarrow1-x=\sqrt{x^2-1}\Rightarrow\left(1-x\right)^2=x^2-1\Leftrightarrow2-2x=0\Leftrightarrow x=1\)
Vậy: \(x=1\text{ là nghiệm (nguyên) duy nhất của phương trình.}\)
1) \(\left(x+\sqrt{x^2+\sqrt{2005}}\right)\left(\sqrt{x^2+\sqrt{2005}}-x\right)=\sqrt{2005}\)
Kết hợp với giả thiết ta được:
\(\sqrt{x^2+\sqrt{2005}}-x=y+\sqrt{y^2+\sqrt{2005}}\)
suy ra: đpcm
2) \(\left(x+\sqrt{x^2+\sqrt{2005}}\right)\left(y+\sqrt{y^2+\sqrt{2005}}\right)=\sqrt{2005}\)
Ta có: \(\hept{\begin{cases}\left(x+\sqrt{x^2+\sqrt{2005}}\right)\left(\sqrt{x^2+\sqrt{2005}}-x\right)=\sqrt{2005}\\\left(y+\sqrt{y^2+\sqrt{2005}}\right)\left(\sqrt{y^2+\sqrt{2005}}-y\right)=\sqrt{2005}\end{cases}}\)
Kết hợp với giả thiết ta có:
\(\hept{\begin{cases}\sqrt{x^2+\sqrt{2005}}-x=y+\sqrt{y^2+\sqrt{2005}}\\\sqrt{y^2+\sqrt{2005}}-y=x+\sqrt{x^2+\sqrt{2005}}\end{cases}}\)
suy ra: \(x+y=-\left(x+y\right)\)
\(\Rightarrow\)\(S=x+y=0\)