
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


biểu thức dã cho <=> ( x+\(\sqrt{x^2+2006}\) ) (\(x-\sqrt{x^2+2006}\)) (y+\(\sqrt{y^2+2006}\)) =2006 (x-\(\sqrt{x^2+2006}\))
=> - 2006 ( y + \(\sqrt{y^2+2006}\)) = 2006 ( x-\(\sqrt{x^2+2006}\))
=>y + \(\sqrt{y^2+2006}\) = \(\sqrt{x^2+2006}\) - x
=>y = \(\sqrt{x^2+2006}\) - x - \(\sqrt{y^2+2006}\) (1)
TT ta có biểu thức đã cho<=>
\(\left(x+\sqrt{x^2+2006}\right)\left(y+\sqrt{y^2+2006}\right)\left(y-\sqrt{y^2+2006}\right)=2006\) (y-\(\sqrt{y^2+2006}\))
<=> -2006 (x+\(\sqrt{x^2+2006}\)) = 2006 (\(y-\sqrt{y^2+2006}\))
<=>x+\(\sqrt{x^2+2006}\) =\(\sqrt{y^2+2006}\) - y
<=>x =\(\sqrt{y^2+2006}-\sqrt{x^2+2006}-y\) (2)
từ (1) và (2)=>x+y= - y - x
=>2 (x+y) = 0 => x+y = 0

a/ ĐKXĐ: ...
Đặt \(\sqrt{x+2006}=a\ge0\Rightarrow a^2-x=2006\)
Pt trở thành:
\(x^2+a=a^2-x\)
\(\Leftrightarrow x^2-a^2+x+a=0\)
\(\Leftrightarrow\left(x+a\right)\left(x-a+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=-x\\a=x+1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+2006}=-x\left(x\le0\right)\\\sqrt{x+2006}=x+1\left(x\ge-1\right)\end{matrix}\right.\) (1)
\(\Leftrightarrow\left[{}\begin{matrix}x+2006=x^2\\x+2006=\left(x+1\right)^2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x^2-x-2006=0\\x^2+x-2005=0\end{matrix}\right.\)
Nhớ loại nghiệm của từng pt phù hợp với (1)
b/ ĐKXĐ: ...
Đặt \(\sqrt{1-\sqrt{x}}=a\Rightarrow\sqrt{x}=1-a^2\Rightarrow x=\left(1-a^2\right)^2\) (với \(0\le a\le1\))
\(\left(1-a^2\right)^2=\left(2005-a^2\right)\left(1-a\right)\)
\(\Leftrightarrow\left(1+a\right)^2\left(1-a\right)^2=\left(2005-a^2\right)\left(1-a\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}a=1\\\left(1-a\right)\left(1+a\right)^2=2005-a^2\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow a^3-a+2004=0\)
Do \(0\le a\le1\Rightarrow a^3-a+2004>0\Rightarrow\) pt vô nghiệm
Vậy pt có nghiệm duy nhất \(x=0\)

\(ĐK:\left\{{}\begin{matrix}x-2008\ge0\\2008-x\ge0\\x-2007>0\end{matrix}\right.\Leftrightarrow x=2008\)
Vậy PT có nghiệm \(x=2008\)

Đặt x -2006 = y
pt <=> \(\frac{y^2-y\left(y-1\right)+\left(y-1\right)^2}{y^2+y\left(y-1\right)+\left(y-1\right)^2}=\frac{19}{49}\)
<=> \(\frac{y^2-y^2+y+y^2-2y+1}{y^2+y^2-y+y^2-2y+1}=\frac{19}{49}\)
<=> \(\frac{y^2-y+1}{3y^2-3y+1}=\frac{19}{49}\)
<=> \(49y^2-49y+49=57y^2-57y+19\)
<=> \(8y^2-8y-30=0\)
<=> \(4y^2-4y+15=0\)
Giải tiếp nha

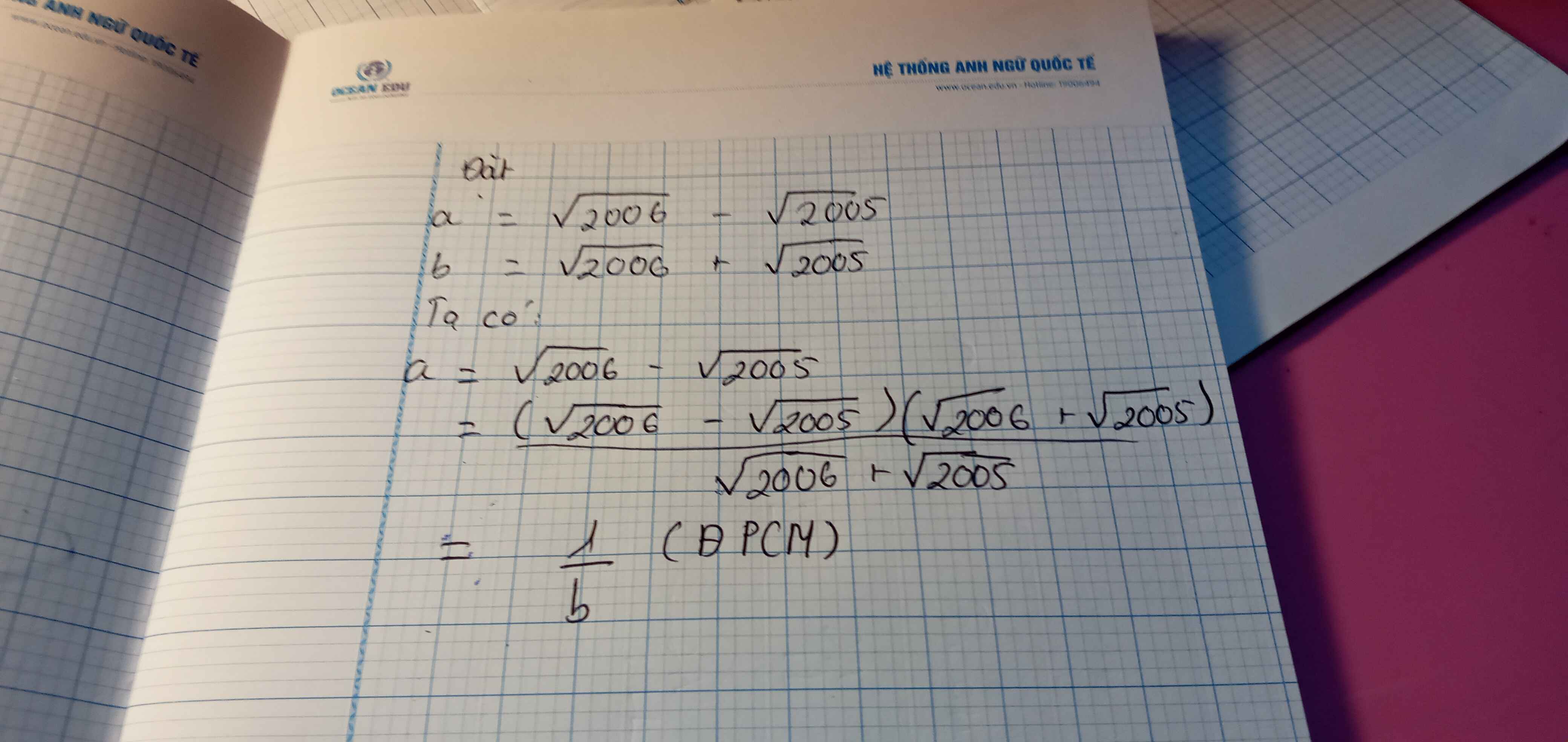
Đặt \(a=\sqrt{2006}-\sqrt{2005};b=\sqrt{2006}+\sqrt{2005}\)
Ta có
\(a=\sqrt{2006}-\sqrt{2005}=\dfrac{\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)}{\sqrt{2006}+\sqrt{2005}}=\dfrac{1}{b}\)
\(\RightarrowĐfcm\)

Điều kiện \(x^2-1\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}x\le-1\\x\ge1\end{matrix}\right.\)
Đặt \(x-\sqrt{x^2-1}=a\) thì ta có pt trở thành:
\(\left(1+a\right)^{2005}+\left(1+\dfrac{1}{a}\right)^{2005}=2^{2006}\)
Ta có:
\(\left(1+a\right)^{2005}+\left(1+\dfrac{1}{a}\right)^{2005}\ge2^{2005}\left(\sqrt{a^{2005}}+\dfrac{1}{\sqrt{a^{2005}}}\right)\ge2^{2006}\)
Đấu = xảy ra khi a = 1 hay
\(x-\sqrt{x^2-1}=1\)
\(\Leftrightarrow x=1\)
Ta có \(\left(x+\sqrt{x^2+2006}\right)\left(y+\sqrt{y^2+2006}\right)=2006\)nên \(\left(\sqrt{x^2+2006}-x\right)\left(x+\sqrt{x^2+2006}\right)\left(y+\sqrt{y^2+2006}\right)=2006.\left(\sqrt{x^2+2006}-x\right)\)\(2006.\left(y+\sqrt{y^2+2006}\right)=2006.\left(\sqrt{x^2+2006}-x\right)\)suy ra \(y+\sqrt{y^2+2006}=\sqrt{x^2+2006}-x\)(1) Tương tự ta có \(x+\sqrt{x^2+2006}=\sqrt{y^2+2006}-y\) (2) cộng (1) và (2) vế với vế ta được
x+y = -(x+y) hay suy ra 2(x+y) = 0 \(\Rightarrow\) x+y = 0