Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là A
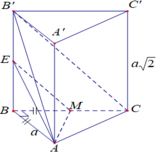
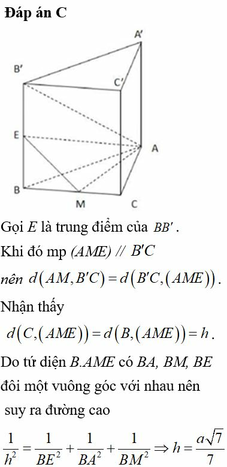
Gọi E là trung điểm của B B ' . Khi đó B ' C / / A M E ⇒ d A M ; B ' C = d B ' C ; A M E .
Mặt khác d B ; A M E = d C ; A M E . Gọi h = d B ; A M E
Vì tứ diện B A M E có B A ; B M ; B E đôi một vuông góc với nhau.
⇒ 1 h 2 = 1 B A 2 + 1 B M 2 + 1 B E 2 ⇒ 1 h 2 = 1 a 2 + 4 a 2 + 2 a 2 = 7 a 2 ⇒ h = a 7 7 ⇒ d B ' C ; A M = a 7 7 .

Đáp án D
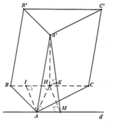
Chọn hệ trục tọa độ như hình vẽ
A 0 ; a ; a 2 , M a 2 ; 0 ; a 2 , B ' 0 ; 0 ; 0 ; , C a ; 0 ; a 2 A M → a 2 ; - a ; 0 , B ' C → a ; 0 ; a 2 ⇒ A M → , B ' C → = - a 2 2 ; - a 2 2 ; a 2 B ' M → a 2 ; 0 ; a 2
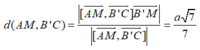


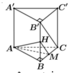
Lời giải.
Gọi H là trung điểm của BB' => HM//B'C
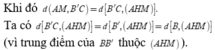
Theo đề, ABC.A'B'C' là lăng trụ đứng và ∆ ABC vuông tại B (vì AB = BC = a)
=> tứ diện BAHM có BA, BH, BM đôi một vuông góc nhau. Khi đó
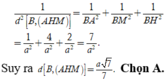

Đáp án A

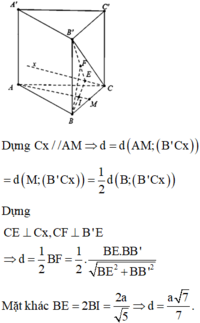
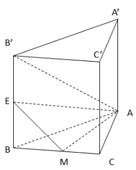
Gọi E là trung điểm của B B ' ⇒ M E / / B ' C ⇒ A M E / / B ' C
⇒ d A M ; B ' C = d B ' C ; A M E = d C ; A M E
Vì B C ∩ A M E = M , B M = M C ⇒ d C ; A M E = d B ; A M E
Gọi h là khoảng cách từ B đến mặt phẳng (AME).
Do tứ diện BAME có BA, BM, BE đôi một vuông góc nên
1 h 2 = 1 B A 2 + 1 B M 2 + 1 B E 2 = 1 a 2 + 4 a 2 + 2 a 2 = 7 a 2
Vậy d A M , B ' C = a 7
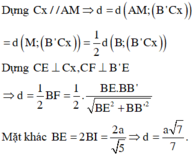
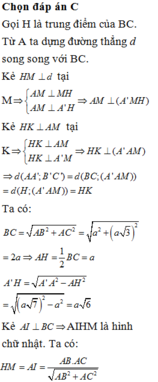


Đáp án D
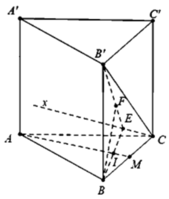
Chọn hệ trục tọa độ như hình vẽ
A ( 0 ; a ; a 2 ) , M ( a 2 ; 0 ; a 2 ) , B ' ( 0 ; 0 ; 0 ) , C ( a ; 0 ; a 2 ) A M → ( a 2 ; − a ; 0 ) , B ' C → ( a ; 0 ; a 2 ) ⇒ [ A M → , B ' C → ] = ( − a 2 2 ; − a 2 2 ; a 2 ) B ' M → ( a 2 ; 0 ; a 2 ) d ( A M , B ' C ) = [ A M → , B ' C → ] B ' M → [ A M → , B ' C → ] = a 7 7