Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là C.
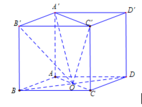
Ta có: V O . A , B , C , = 1 2 V O . A , B , C , D , ; V O . A , B , C , D , 1 3 V A B C D . A , B , C , D ,
V O . A , B , C , = 1 6 V A B C D . A , B , C , D , ⇒ V O . A , B , C , V A B C D . A , B , C , D = 1 6

Đáp án B.
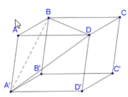
Ta có V A C B ' D ' = V A B C D . A ' B ' C ' D ' - V D ' . A C D - V C . A ' B ' D ' - V B ' . A B C
= V A B C D . A ' B ' C ' D ' - 4 . 1 6 V A B C D . A ' B ' C ' D ' = 1 3 V V A B C D . A ' B ' C ' D ' .

Đáp án B
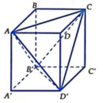
Nhìn hình vẽ ta thấy sẽ khó tính trực tiếp thể tích của khối tứ diện A C B ' D ' , do vậy ta sẽ tính gián tiếp.
Ta tính thể tích các khối tứ diện A C D D ' ; A A ' D ' B ' ; A B C B ' ; C C ; B ' D ' . Sau đó lấy thể tích khối hộp trừ đi tổng thể tích các khối trên.
Ta nhận thấy cả bốn khối tự diện A C D D ' ; A A ' D ' B ' ; A B C B ' ; C C ; B ' D ' đều có thể tích bằng nhau và bằng V 1 = 1 3 A A ' . 1 2 S A B C D = 1 6 V A B C D . A ' B ' C ' D ' = 1 6 V
Thể tích của khối tứ diện A C B ' D ' bằng V 2 = V − 4 6 V = V 3
Tỉ số cần tìm là 3. Ta chọn B

Phương pháp:
- Dựng mặt phẳng chứa B'G và song song với C'D.
- Xác định khối đa diện và tính thể tích bằng cách cộng trừ thể tích các khối đa diện đơn giản.
Cách giải:
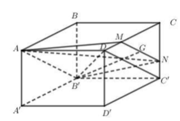

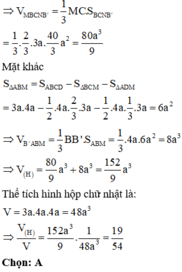

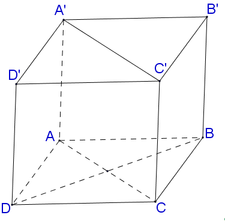
Đáp án A
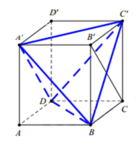
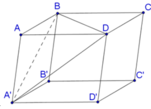
Gọi V là thể tích của khối hộp A B C D . A ' B ' C ' D ' . Khi đó
V A B C D . A ' B ' C ' D ' = V A ' . A B C D + V C . B C D + V D . A ' C ' D ' + V B . A ' B ' C ' + V A . C ' B D
= V 6 + V 6 + V 6 + V 6 + V A . C ' B D = 2 V 3 + V A ' . C ' B D → V A ' . C ' B D = V 3
Vậy tỉ số cần tính là V A ' C ' B D V A B C D . A ' B ' C ' D ' = 1 3 .
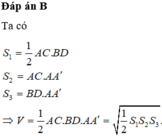
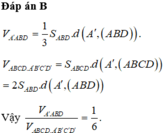
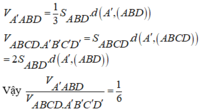
Đáp án B