Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
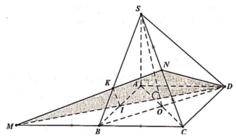
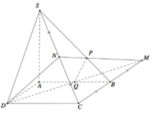
Gọi ![]()
Khi đó góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 45o![]()
Ta có: ∆BAD đều ![]()
Thể tích khối chóp S.ABCD bằng: 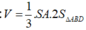
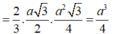
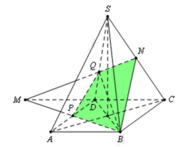
Ta có: N là trung điểm SC nên 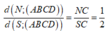
Thể tích khối chóp N.MCD bằng thể tích khối chóp N.ABCD bằng: ![]()
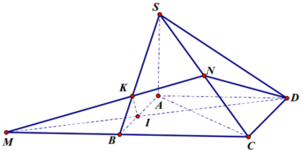
Ta có K là trọng tâm tam giác SMC
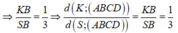
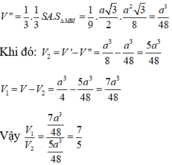

Chọn C

Ta có: α ∩ ( S C D ) = M N ⇒ M N / / C D .
Do đó α là (ABMN).
Mặt phẳng α chia khối chóp thành 2 phần có thể tích bằng nhau là
V S . A B M N = V A B C D M N ⇒ V S . A B M N = 1 2 . V S . A B C D 1
Ta có:
V S . A B C = V S . A C D = 1 2 V S . A B C D
Đặt S N S D = x với (0<x<1), khi đó theo Ta-let ta có S N S D = S M S C = x .
Mặt khác
V S . A B M V S . A B C = S A S A . S B S B . S M S C = x ⇒ V S . A B M = x 2 V S . A B C D
V S . A M N V S . A C D = S A S A . S M S C . S N S D = x 2 ⇒ V S . A M N = x 2 2 V S . A B C D
⇒ V S . A B M N = V S . A B M + V S . A M N = ( x 2 + x 2 2 ) . V S . A B C D 2
Từ (1), (2) suy ra
x 2 + x 2 2 = 1 2 ⇔ x 2 + x - 1 = 0
x = - 1 - 5 2 v à x = - 1 + 5 2
Đối chiếu điều kiện của x ta được S N S D = - 1 + 5 2
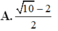
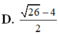

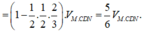
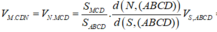
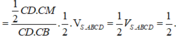
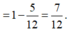
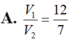
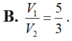
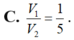
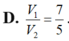
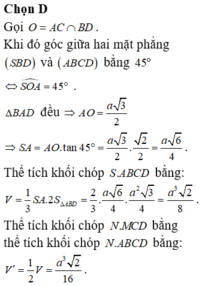
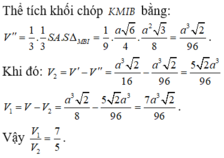
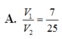
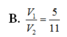
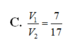
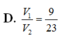


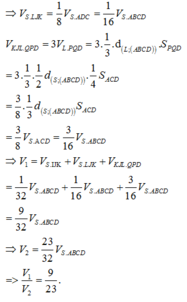
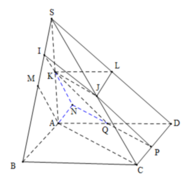
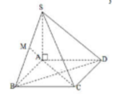
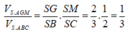
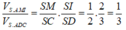
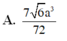
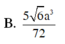
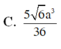
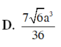



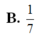
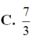
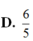
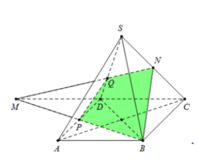

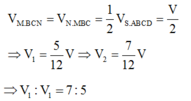
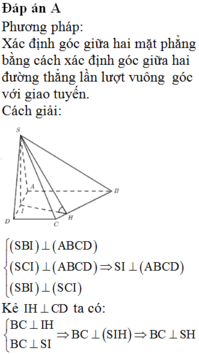
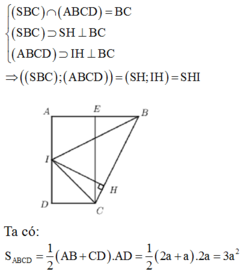

Chọn A
Vì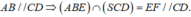
Chia khối chóp S.ABEF thành hai khối chóp tam giác S.AEF, S.ABE có