Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D


Thể tích khối chóp N.MCD bằng thể tích khối chóp N.ABCD:

FOR REVIEW |
Tam giác cân có một góc bằng 60 ° thì là tam giác đều. |

Chọn đáp án C
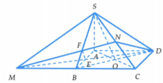
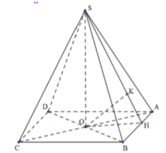
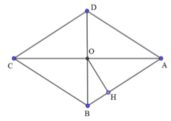
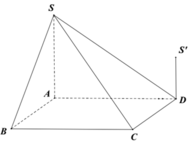
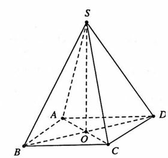
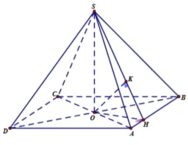
Gọi O là giao điểm của AC và BD
Ta có
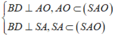
![]()
![]()
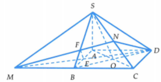
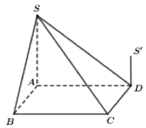
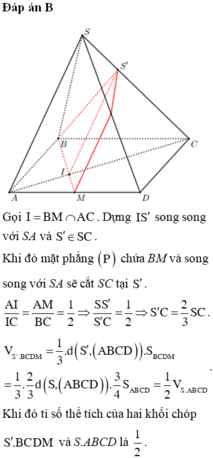
⇒ Thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng (MND) là tứ giác DEFN.
Suy ra V 1 = V S . A D E F N và V 2 = V B C D E F N
Từ giả thiết ta có ∆ A B D đều cạnh a
![]()
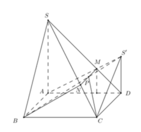
Thể tích khối chóp N.MCD là
V N . M C D = 1 3 d N ; M C D . S ∆ M C D = a 3 4
Ta có F là trọng tâm của ∆ S M C nên M F M N = 2 3 ; E là trung điểm của MD nên M E M D = 1 2
Áp dụng công thức tính thể tích ta có:
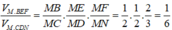
![]()
Thể tích khối chóp S.ABCD là
V S . A B C D = 1 3 . S A . S A B C D = a 3 4
Suy ra V 1 = V S . A D E F N = V S . A B C D - V 2 = a 3 24
Vậy V 1 V 2 = 1 5




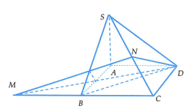

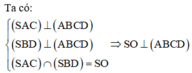

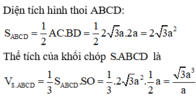


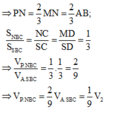


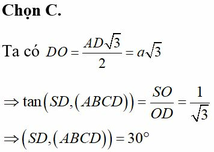

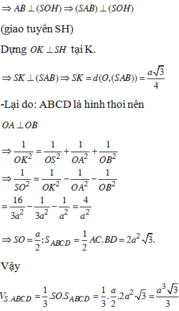
Đáp án C
Ta có: S A O B = 1 4 S A B C D
Do đó V S . A B C D V S . A O B = S A B C D . S H S A O B . S H = 4