Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

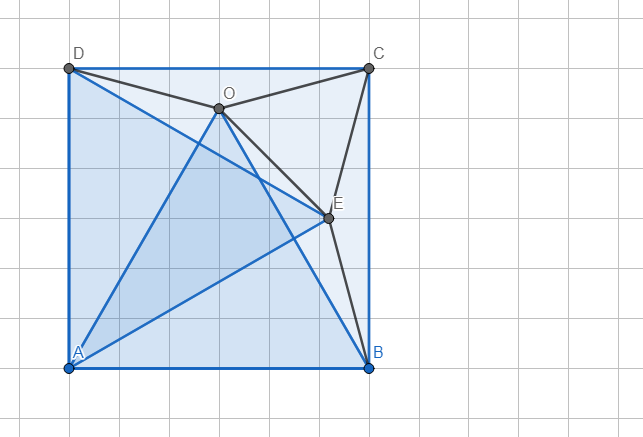
*Dựng △ADE đều.
\(\widehat{ODC}=\widehat{OCD}=15^0\Rightarrow\)△DOC cân tại O.
\(\Rightarrow OD=OC;\widehat{DOC}=180^0-2\widehat{ODC}=180^0-2.15^0=150^0\)
\(\widehat{BAE}=\widehat{CDE}=90^0-\widehat{ADE}=90^0-60^0=30^0\)
\(AB=AE=DE=DC=AD\).
\(\Rightarrow\)△DCE cân tại D, △ABE cân tại A.
\(\Rightarrow\widehat{DCE}=\widehat{ABE}=\dfrac{180^0-\widehat{BAE}}{2}=\dfrac{180^0-30^0}{2}=75^0\).
\(\Rightarrow\widehat{ECB}=\widehat{EBC}=90^0-\widehat{DCE}=90^0-75^0=15^0\)
\(\widehat{OCE}=90^0-\widehat{OCD}-\widehat{BCE}=90^0-15^0-15^0=60^0\)
△DOC và △BEC có: \(\widehat{ODC}=\widehat{EBC}=15^0;\widehat{OCD}=\widehat{ECB}=15^0;DC=BC\)
\(\Rightarrow\)△DOC=△BEC (g-c-g)
\(\Rightarrow OD=BE=OC=EC\)
\(\Rightarrow\)△OCE cân tại C mà \(\widehat{OCE}=60^0\)
\(\Rightarrow\)△OCE đều.
\(\widehat{OEB}=360^0-\widehat{OEC}-\widehat{BEC}=360^0-60^0-150^0=150^0\)
\(OE=CE=EB\Rightarrow\)△OEB cân tại E.
\(\Rightarrow\widehat{OBE}=\dfrac{180^0-\widehat{OEB}}{2}=\dfrac{180^0-150^0}{2}=15^0\)
\(\widehat{OBA}=90^0-\widehat{OBE}-\widehat{CBE}=90^0-15^0-15^0=60^0\)
Mà △OAB cân tại O \(\Rightarrow\)△OAB đều.
Vẽ ra phía ngoài hình vuông 1 tam giác đều ABE. Vì EA=EB; MA=MB nên EM là đường trung trực AB, suy ra ˆMEB=30∘
VÌ ΔEBM=ΔCBM(c.g.c), suy raˆMCB=ˆMEB=30∘⇒ˆMCD=60∘(1).
Mặt khác, ΔAMD=ΔBMC(c.g.c), suy ra: MD=MC (2)
Từ (1) & (2) =>ΔMCDđều (đpcm)
tam giác AMD= BMC (c-g-c)
trên nửa mặt phẳng bờ AD chứa BC kẻ Ax và Dy sao cho Ax, Dy tạo vs AD các góc 15 độ, chứng cắt nhau tại J
Tam giác AJD có góc DAJ=JDA=15
=> t,g ADJ cân tại J
ta có t.g AJDJ= ABM (g-c-g)
=>AJ=AM
=> t.g AMJ cân tại A mà MAJ=60 (DAJ+JAM+MAB=90)
=> t.g ẠM đều
=>JA=JM
ta có MJS=AMJ+MAJ=60+60=120 (góc ngoài t.g)
tương tự ta có SJD=30
vậy MJD=SJM+SJD=120+30=150
lại có t.g JDM có JD=JM (cùng= JA)
=> JDM cân tại J mà góc MJD=120
=>JDM=15
ta có góc ADJ + JDM+MDC=90
15+15+mdc=90
MDC =60
tam giác MCD cân mà có góc D =60
=> MCD là tam giác đều