NL
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NL
1
BM
1
5 tháng 10 2020
Vì \(\tan MAB=\frac{MB}{AB}=\frac{1}{2}\Rightarrow\widehat{MAB}=26,5°\)Tương tự có \(\widehat{NAD}=26,5°\)
\(\Rightarrow\widehat{MAN}=37°\Rightarrow\cos MAN=\cos37\approx0,79\)
PT
1
CM
17 tháng 10 2018
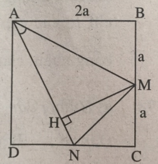
Kẻ đường cao MH của tam giác cân AMN. Ta có sin ∠ (NAM) = HM/AM và diện tích tam giác AMN là S A M N = 1/2AN.MH = 1/2AN.AM.sin(NAM) = 1/2 A N 2 .sin(NAM) = 1/2( A D 2 + D N 2 ). sin(NAM) = ( 5 a 2 )/2 sin(NAM).
30 tháng 10 2023
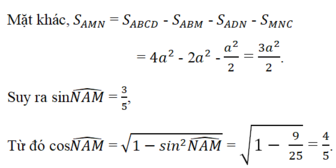
ABCD là hình vuông
=>AC là phân giác của \(\widehat{BAD}\) và CA là phân giác của \(\widehat{BCD}\) và BD là phân giác của \(\widehat{ABC}\); DB là phân giác của \(\widehat{ADC}\)
=>\(\widehat{BAC}=\widehat{BCA}=\widehat{DAC}=\widehat{DCA}=\widehat{ABD}=\widehat{DBC}=\widehat{ADB}=\widehat{CDB}=45^0\)
Xét tứ giác EABN có
\(\widehat{EAN}=\widehat{EBN}=45^0\)
nên EABN là tứ giác nội tiếp
EABN là tứ giác nội tiếp
=>\(\widehat{ANE}=\widehat{ABE}=45^0\)
\(\widehat{EAN}+\widehat{ENA}=45^0+45^0=90^0\)
=>NE\(\perp\)AM tại E