

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



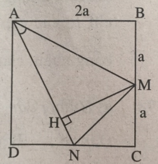
Kẻ đường cao MH của tam giác cân AMN. Ta có sin ∠ (NAM) = HM/AM và diện tích tam giác AMN là S A M N = 1/2AN.MH = 1/2AN.AM.sin(NAM) = 1/2 A N 2 .sin(NAM) = 1/2( A D 2 + D N 2 ). sin(NAM) = ( 5 a 2 )/2 sin(NAM).

A B C D M N 2a H
a) Gọi H là giao điểm của AM và BN
\(\Delta ABMvà\Delta BCN\) có:
AB=BC(ABCD là hình vuông)
góc ABM=góc BCN=90o
BM=CN=1/2 cạnh hình vuông
=>\(\Delta ABM=\Delta BCN\left(c-g-c\right)\)
=> góc AMB= góc BNC
mà BNC+HBC=90o
=>AMB+HBC=900
=> góc BHM=900
=>\(AM\perp BN\)(đpcm)
b)tam giác ABM và tam giác ADN có:
AB=AD(ABCD là hình vuông )
góc ABM=góc ADN=90o
BM=DN=1/2 cạnh hình vuông
=> tam giác ABM= tam giác ADN(c.g.c)
=> AM=AN=\(\sqrt{AD^2+DN^2}=\sqrt{\left(2DN\right)^2+DN^2}=DN\sqrt{5}=a\sqrt{5}\)
tam giác ABH vuông tại B có BH vuông góc với AM
=> AH.AM=AB2
\(\Rightarrow AH=\dfrac{AB^2}{AM}=\dfrac{4a^2}{a\sqrt{5}}=\dfrac{4a}{\sqrt{5}}\)
=> cos MAN = \(\dfrac{AH}{AN}=\dfrac{4a}{\sqrt{5}}:a\sqrt{5}=\dfrac{4}{5}\)

Vì \(\tan MAB=\frac{MB}{AB}=\frac{1}{2}\Rightarrow\widehat{MAB}=26,5°\)Tương tự có \(\widehat{NAD}=26,5°\)
\(\Rightarrow\widehat{MAN}=37°\Rightarrow\cos MAN=\cos37\approx0,79\)

A B C D F E M
Xét tam giác vuông là tam giác BEC và tam giác DCF có CD = BC , BE = CF = 1/2a
=> Tam giác BEC = tam giác DCF (hai cạnh góc vuông)
=> góc CDF = góc BCE mà góc CDF + góc DFC = 90 độ
=> góc ECF + góc DFC = 90 độ hay góc DMC = 90 độ => CE vuông góc DF
Ta chứng minh được tam giác MDC đồng dạng tam giác CDF (g.g)
Áp dụng định lí Pytago có \(DF=\sqrt{CD^2+FC^2}=\sqrt{a^2+\frac{a^2}{4}}=\frac{a\sqrt{5}}{2}\)
\(S_{CDF}=\frac{1}{2}CD.CF=\frac{1}{2}a.\left(\frac{a}{2}\right)=\frac{a^2}{4}\)
Suy ra \(\frac{S_{MDC}}{S_{CDF}}=\left(\frac{CD}{DF}\right)^2=\left(\frac{a}{\frac{a\sqrt{5}}{2}}\right)^2=\left(\frac{2}{\sqrt{5}}\right)^2=\frac{4}{5}\)
\(\Rightarrow S_{MDC}=\frac{4}{5}S_{CDF}=\frac{4}{5}.\frac{a^2}{4}=\frac{a^2}{5}\)

C D B A H N M
a) Kẻ CH vuông góc với AB ( H thuộc AB )
Ta có : \(BH=\frac{AB-CD}{2}=\frac{30-10}{2}=10\left(cm\right)\)
Ta lại có :
\(\cos\widehat{B}=\frac{BH}{BC}\)
\(\Rightarrow BC=\frac{10}{\cos60^o}\)
Vì cos 60o = \(\frac{1}{2}\)
\(\Rightarrow BC=10.2=20\left(cm\right)\)
b) Vì ABCD là hình thang cân
M , N lần lượt là trung điểm của AB , Cd
=>MN vuông góc với CD và AB
=> MN = CH
Theo định lí py-ta-go ta có : \(CH=\sqrt{BC^2-BH^2}=\sqrt{20^2-10^2}=10\sqrt{3}\left(cm\right)\)
=> MN = \(10\sqrt{3}\)

Chi tiết \(BM=DN=\dfrac{a}{3}\) hoàn toàn không cần thiết
a.
Ta có: \(AC\perp BD\) tại O (2 đường chéo hình vuông) \(\Rightarrow O\) thuộc đường tròn đường kính AB
\(AH\perp BH\) (gt) \(\Rightarrow\) H thuộc đường tròn đường kính AB
\(\Rightarrow\) 4 điểm A,B,O,H cùng thuộc đường tròn đường kính AB hay tứ giác ABHO nội tiếp
Hoàn toàn tương tự, 4 điểm ADKO cùng thuộc đường tròn đường kính AD nên tứ giác ADKO nội tiếp
b.
Trong tam giác vuông ABM vuông tại B với đường cao BH, áp dụng hệ thức lượng:
\(AB^2=AH.AM\)
Tương tự, trong tam giác vuông ADN:
\(AD^2=AK.AN\)
Mà \(AB=AD=a\Rightarrow AH.AM=AK.AN\Rightarrow\dfrac{AH}{AN}=\dfrac{AK}{AM}\) (đpcm)