K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
1 tháng 1 2017
Ta có DAOK = DCOH Þ OK =OH, DDOE = DBOF Þ OE = OF Þ EHFK là hình bình hành


29 tháng 8 2021
ABCD là hbh=> AD//BC=> góc DAC= góc ACB và AO=OC
Xét tam giác AOE và tam giác COF ta có
góc AOE = góc COF (2 góc đối xừng)
AO=OC
góc DAC= góc ACB
=> tam giác AOE = tam giác COF=> OE=OF
CHứng minh tương tự ta có tam giác AOK= tam giác COH=> OK=OH
Xét tứ giác EHFK có EH và FK là 2 đường chéo cắt nhau tại O
lại có OE=OF
OH=OK
=> EHFk là hình bình hành (do 2 đường chéo cắt nhau tại trung điểm mỗi đường)
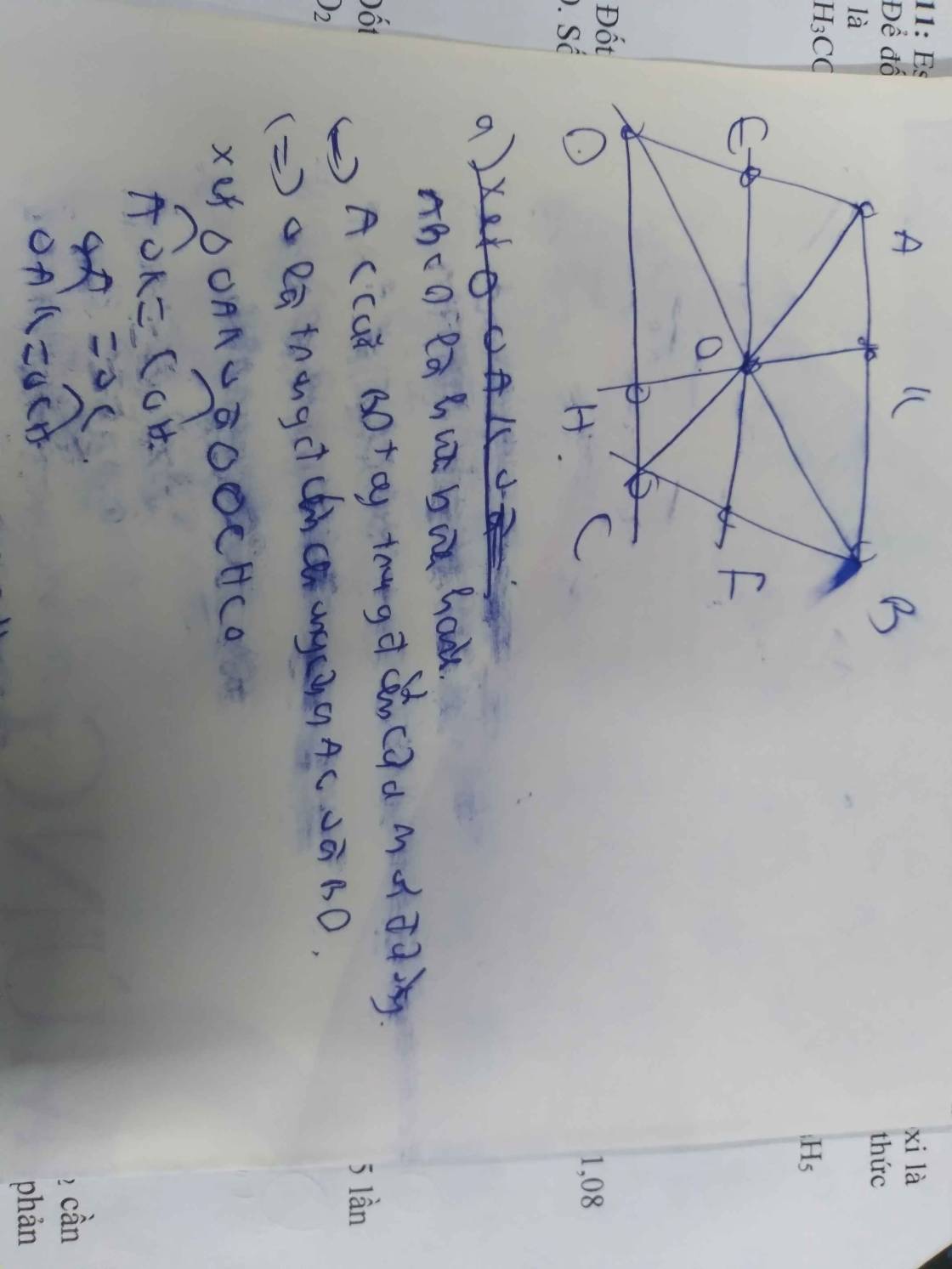


a: Xét ΔEOD và ΔFOB có
\(\widehat{EDO}=\widehat{FBO}\)
DO=BO
\(\widehat{EOD}=\widehat{FOB}\)
Do đó: ΔEDO=ΔFBO
Suy ra: ED=FB