Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔADE và ΔCBF có
\(\widehat{ADE}=\widehat{CBF}\)
AD=CB
\(\widehat{A}=\widehat{C}\)
Do đó: ΔADE=ΔCBF
Suy ra: DE=BF

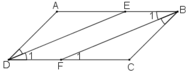
a) Ta có:
+ ABCD là hình bình hành ⇒ AB // CD ⇒ 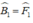 (Hai góc đồng vị) (1)
(Hai góc đồng vị) (1)
+ DE là tia phân giác của góc D
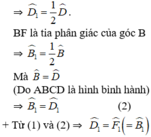
Mà hai góc này ở vị trí đồng vị ⇒ DE // BF (đpcm)
b) Tứ giác DEBF có:
DE // BF (chứng minh ở câu a)
BE // DF (vì AB // CD)
⇒ DEBF là hình bình hành.

ghét hè. mi cứ đi hỏi lung tung nik. trách chi bựa đến giừ bài tập làm đc
kéo dài DA và CB cắt nhau tại K
AB là đường trung bình ( AB//DC và 2AB = DC)
=> B là trung điểm KC
=> DB là trung tuyến ΔKDC vuông tại D
=> DB = BC = DC
=> tam giác DBC đều
Vậy góc KCD= 60độ
tổng 4 góc trong tứ giác ABCD = 360độ
=> góc ABC = 120độ
cách 2
Kẻ BH⊥CD suy ra tứ giác ABHD là hình chữ nhật
nên ^ABH=90* (1)
Xét ∆BHC vuông tại H có HC=1/2 BC nên ^HBC=30* (2)
Từ (1) và (2) suy ra ^ABC=^ABH+^HBC=90*+30*=120*

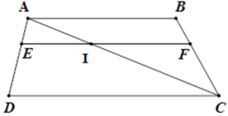
Gọi I là giao điểm của AC và EF.
Xét tam giác ACB có IF // AB nên theo định lý Ta-lét ta có
B F B C = A I A C = A E A D = 4 12 = 1 3 nên BF = 1 3 .BC = 1 3 .15 = 5 (cm)
Đáp án: B

bạn vẽ hình nhé
a) ta có ABCD là hbh nên góc D = góc B
=> góc EDF = 1/2 góc D = 1/ góc B = góc EBF
ta lại có: góc EBF bù góc BFD (là hai góc trong cùng phía của hai đường thẳng // - AB//DC)
nên góc EDF cũng bù với góc BFD suy ra DE // DF ( có hai góc trong cùng phia bù nhau)
b) xét tư giác DEBF có
BE// DF (gt)
DE// BF (cmt)
vậy DEBF là hình bình hành
