
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Sửa đề: Tia AD là tia phân giác của góc HAC
Xét ΔBAD có BA=BD(gt)
nên ΔBAD cân tại B(Định nghĩa tam giác cân)
Ta có: \(\widehat{BAD}+\widehat{CAD}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)(ΔBAD cân tại B)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là tia phân giác của \(\widehat{HAC}\)(đpcm)
b) Xét ΔAKD vuông tại K và ΔAHD vuông tại H có
AD chung
\(\widehat{KAD}=\widehat{HAD}\)(AD là tia phân giác của \(\widehat{KAH}\))
Do đó: ΔAKD=ΔAHD(cạnh huyền-góc nhọn)
Suy ra: AK=AH(hai cạnh tương ứng)

a: Ta có:ΔABC cân tại A
mà AH là đường cao
nên AH vừa là đường trung tuyến vừa là đường phân giác
b: BC=8cm
nên BH=CH=4cm
=>AH=3cm
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra:HD=HE
hay ΔHDE cân tại H

a)Ta có:BD=BA(gt)
⇒ΔBAD cân tại B
⇒góc BAD=góc BDA
Trong ΔADH vuông tại H,có:
góc DAH+góc ADH=90 độ
Mà góc BAD+góc DAK=90 độ
⇒DAH+ADH=BAD+DAK
Mà góc ADH=góc BAD(cmt)
⇒Góc DAH=góc DAK
⇒AD là tia phân giác của góc HAC
b)Xét ΔADH và ΔADK,có:
góc H=góc K=90 độ
AD chung
góc DAH=góc DAK
⇒ΔADH=ΔADK(ch-gn)
⇒AH=AK(2 cạnh t/ứ)
c)Ta có:KC<DC(ΔKDC vuông tại K)
Mà KC=AC-AK
DC=BC-BD
⇒AC-AK<BC-BD
⇒ AC + BD < BC + AK
Mà BD=BA(gt)
⇒AK = AH (cmt)
⇒AB+AC<BC+AH
#Cừu

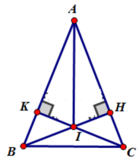

Xét ΔABH vuông tại H và ΔACK vuông tại K có:
AB = AC (Do ΔABC cân tại A)
góc A chung
Nên ΔABH = ΔACK (cạnh huyền – góc nhọn) ⇒ AH = AK (hai cạnh tương ứng).

tự kẻ hình
AB = 6 (gt) => AB^2 = 6^2 = 36
AC = 8 (gt) => AC^2 = 8^2 = 64
=> AB^2 + AC^2 = 36 + 64 = 100
BC = 10 (gt) => BC^2 = 10^2 = 100
=> AB^2 + AC^2 = BC^2
=> AH^2 + BC^2 = AH^2 = AH^2 + AC^2 + AB^2
=> AH^2 + BC^2 > AB^2 + AC^2
=> AH + BC > AB + AC do AH; BC; AB; AC >0
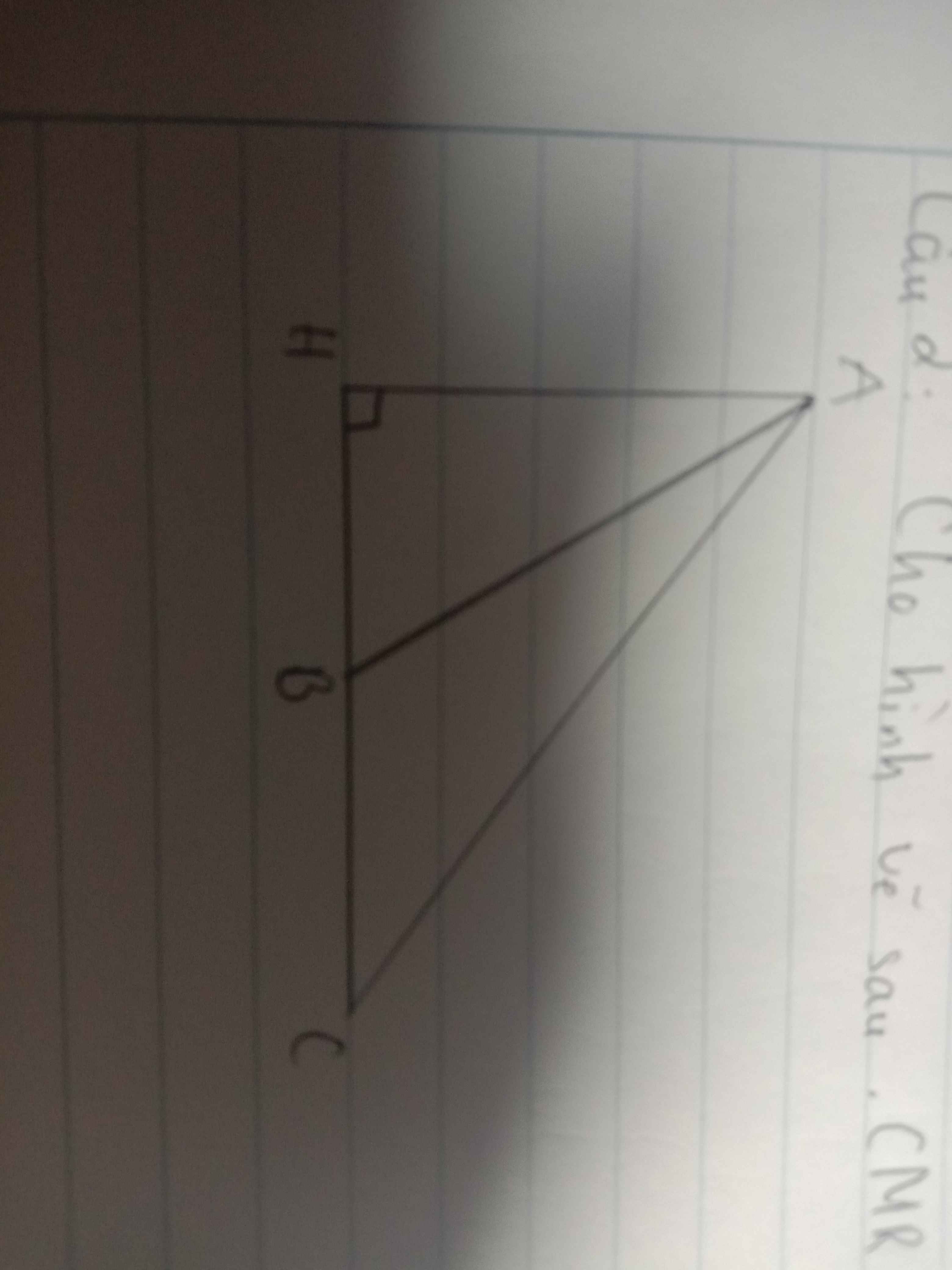 Cho hình vẽ sau. Chứng minh rằng AH<AB<AC
Cho hình vẽ sau. Chứng minh rằng AH<AB<AC
hình đâu bạn
Thiếu đề