K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 3 2023
Ta có:
AB đồng dạng với AD với tỉ số tỉ số k = 1 (vì hai cạnh đối sát của hình bình hành bằng nhau và song song).
Vậy diện tích tam giác ABH bằng diện tích tam giác ADK với tỷ số k.
Như vậy: S_ABH = k.S_ADK.
Tuy nhiên, ta cũng có: S_ABH = AB.AH và S_ADK = AD.AK (vì diện tích một tam giác bằng nửa tích các cạnh tạo thành đôi một với nó).
Vậy ta có: AB.AH = AD.AK.
Đây chính là điều cần chứng minh.
QD
6 tháng 6 2016
diện tích tam giác ABC bằng tổng diện tích ba hình tam giác : ABM ; AMN ; ANC.
Diện tích tam giác ABM là :
( 25 x 12 ) : 2 = 150 ( cm2 )
Vì ba tam giác ABM , AMN và ANC có cung chiều cao kẻ từ A nên :
Diện tích tam giác AMN bằng \(\frac{3}{2}\) diện tích tam giác ABM và bằng :
150 x \(\frac{3}{2}\) = 225 ( cm2 )
Diện tích tam giác ANC bằng \(\frac{1}{2}\) diện tích tam giác AMN và bằng :
225 : 2 = 112,5 ( cm2 )
Diện tích tam giác ABC là :
150 + 225 + 112,5 = 487,5 ( cm2 )
đáp số : 487,5 cm2
HQ
Hà Quang Minh
Giáo viên
10 tháng 10 2023
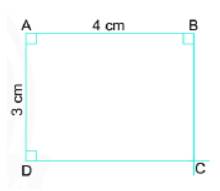
Vẽ đoạn thẳng AB = 4cm.
Sử dụng êke để kẻ đường vuông góc với AB tại A. Trên đường vuông góc này lấy điểm D sao cho đoạn thẳng AD = 3 cm.
Sử dụng êke để kẻ đường vuông góc với AB tại B; kẻ đường vuông góc với AD tại D. Nối hai đường vuông góc này thấy hai đường này cắt nhau tại C.
Ta được, ABCD là hình chữ nhật cần vẽ.
C
1
SK
0