Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C. (D ) = 45o
Ta có : hình thang ABCD CÓ BC//AD
=> ∠ (C )+ ∠ (D )= 180 0 ( hai góc trong cùng phía bù nhau)
mà ∠ C = 3 ∠ D nên 3 ∠ D+ ∠ D= 180 0 => ∠ D= 45 0

Chọn A. ∠ (C ) = 110 0
Ta có : ∠ (A )+ ∠ (D )= 180 0 ( hai góc trong cùng phía)
=> ∠ (D )= 180 0 - ∠ (A )= 180 0 - 70 0 = 110 0
mà ∠ (C )= ∠ (D ) (tính chất hình thang cân ) => ∠ (C )= ∠ (D )= 110 0

Chọn B
Mà ∠ B = ∠ A + 10 ° (2)
nên từ (1) và (2) => ∠ C - 10 ° = ∠ A + 10 ° => ∠ C = ∠ A + 20 °
Ta có: ∠ D = ∠ C + 10 ° => ∠ D = ∠ A + 20 ° + 10 ° => ∠ D = ∠ A + 30 °
Ta có : ∠ A+ ∠ B+ ∠ C+ ∠ D = 360 ° ( tổng bốn góc của tứ giác)
=> ∠ A+ ∠ A + 10 ° + ∠ A + 20 ° + ∠ A + 30 ° = 360 °
=> 4 ∠ A + 60 ° = 360 °
Do đó: ∠ A= 75 °
=> ∠ B = ∠ A + 75 ° + 10 ° = 85 °
=> ∠ C= ∠ A+ 20 ° = 95 °
=> ∠ D= ∠ A+ 30 ° = 105 °

Theo giả thiết ta có: a > b, c > d ⇒ a + c > b + d.
Chọn đáp án B.

Theo giả thiết ta có: a > b, c > d ⇒ a + c > b + d.
Chọn đáp án B.

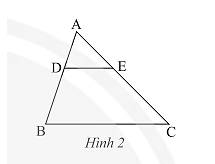
Vì \(DE//BC\) nên theo định lí Thales và hệ quả của định lí Thales ta có:
\(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}};\frac{{BD}}{{AD}} = \frac{{EC}}{{AE}};\frac{{BD}}{{AB}} = \frac{{EC}}{{AC}};\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\).

Câu 1. B) m ≠ ±3
Câu 2. B) 3
Câu 3. C) 8cm
Câu 4. C) AB.DF = AC.DE
Câu 5. B) AC = 6cm
không hiểu chỗ nào ib mình giảng

a: Xét ΔABC có DE//BC
nên AD/AE=AB/AC
b: Xét ΔABC có DE//BC
nên BD/CE=AB/AC
hay \(BD\cdot AC=AB\cdot CE\)
d: \(\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{AD}{AB}\right)^2=\dfrac{AD}{AB}\cdot\dfrac{AE}{AC}\left(ĐPCM\right)\)

a: Xét ΔBAC có BD là phân giác
nên AD/AB=DC/BC
=>AD/6=DC/4
hay AD/3=DC/2
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{3}=\dfrac{DC}{2}=\dfrac{AD+DC}{3+2}=\dfrac{6}{5}=1.2\)
Do đo: AD=3,6(cm)
Xét ΔBAC có ED//BC
nên ED/BC=AD/AC
=>ED/4=3,6/6=3/5
hay ED=2,4(cm)
b: Xét ΔBAD và ΔCAE có
\(\widehat{ABD}=\widehat{ACE}\)
góc BAD chung
Do đó: ΔBAD\(\sim\)ΔCAE
c: Ta có: ΔABD\(\sim\)ΔACE
nên AB/AC=AD/AE
hay \(AB\cdot AE=AD\cdot AC\)
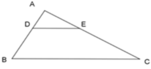
Áp dụng hệ quả định lý Ta-lét, ta có: A D A B = A E A C = D E B C
=> Đáp án A đúng.
+ Vì A D A B = A E A C nên AD.AC = AB.AE
=> Đáp án B sai.
+ Ta có: D E B C = A D A B ≠ A D D B (hệ quả định lý Ta-lét)
=> Đáp án C sai.
+ Ta có: A D D B = D E B C => AD.BC = AB.DE
=> Đáp án D sai.
Đáp án: A