Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

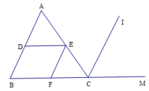
Vì EF // CI nên MCI ^ = CFE ^ (hai góc đồng vị)
Vì DE // BC nên CFE ^ = DEF ^ (hai góc so le trong)
⇒ MCI ^ = DEF ^ (1)
Vì EF // CI nên FEC ^ = ACI ^ (hai góc so le trong) (2)
Mặt khác, ⇒ MCI ^ = ACI ^ (vì CI là tia phân giác của ACM ^ ) (3)
Từ (1), (2), (3) suy ra DEF ^ = FEC ^
Vậy EF là tia phân giác của DEC ^

a: Xét ΔABN và ΔAMN có
AB=AM
góc BAN=góc MAN
AN chung
=>ΔABN=ΔAMN
=>BN=MN
b: Đề bài yêu cầu gì?

a: Xét ΔABN và ΔAMN có
AB=AM
góc BAN=góc MAN
AN chung
=>ΔABN=ΔAMN
=>BN=MN
b: Đề bài yêu cầu gì vậy bạn?

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
b: Xét ΔMAB vuông tại M và ΔMDC vuông tại M có
MB=MC
\(\widehat{MBA}=\widehat{MCD}\)(hai góc so le trong, AB//CD)
Do đó: ΔMAB=ΔMDC
Ta có: \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
\(\widehat{ABC}=\widehat{DCB}\)(hai góc so le trong, AB//CD)
Do đó: \(\widehat{ACB}=\widehat{DCB}\)
=>CB là phân giác của góc ACD

a: Xét ΔBAM và ΔBNM có
BA=BN
góc ABM=góc NBM
BM chung
=>ΔBAM=ΔBNM
b: ΔBAM=ΔBNM
=>AM=NM và góc BNM=góc BAM=90 độ