Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Sửa đề; DH vuông góc EF tại H
a: Xét ΔDHE vuông tại H và ΔDHF vuông tại H có
DE=DF
DH chung
Do đó: ΔDHE=ΔDHF
=>HE=HF
b: Ta có: HE=HF
H nằm giữa E và F
Do đó: H là trung điểm của EF
=>\(HE=HF=\dfrac{EF}{2}=4\left(cm\right)\)
ΔDHE vuông tại H
=>\(DH^2+HE^2=DE^2\)
=>\(DH^2=5^2-4^2=9\)
=>\(DH=\sqrt{9}=3\left(cm\right)\)
c: Ta có: \(DM=MF=\dfrac{DF}{2}\)
\(DN=NE=\dfrac{DE}{2}\)
mà DF=DE
nên DM=MF=DN=NE
Xét ΔDME và ΔDNF có
DM=DN
\(\widehat{MDE}\) chung
DE=DF
Do đó: ΔDME=ΔDNF
=>EM=FN và \(\widehat{DEM}=\widehat{DFN}\)
d: Xét ΔNEF và ΔMFE có
NE=MF
NF=ME
EF chung
Do đó: ΔNEF=ΔMFE
=>\(\widehat{NFE}=\widehat{MEF}\)
=>\(\widehat{KEF}=\widehat{KFE}\)
=>ΔKEF cân tại K

a) Ez bạn tự làm nha, mình làm sơ sơ cũng 3-4 cách rồi.:)
b) Tam giác ABC cân tại A có đường p/g góc A xuất phát từ đỉnh đồng thời là đường trung trực nên \(AD\perp BC\). và BD = CD = BC/2
Xét tam giác ABD vuông tại D (chứng minh trên), theo định lí Pythagoras:
\(AB^2=BD^2+DA^2\Leftrightarrow10^2=\frac{BC^2}{4}+DA^2\)
\(=36+DA^2\Rightarrow AD=8\) (cm) (khúc này có tính nhầm gì thì tự sửa lại nha!)
Theo đề bài ta có AB = AC = 10 < BC = 12
Hay AC < BC. Theo quan hệ giữa góc và cạnh đối diện trong tam giác ABC ta có \(\widehat{ABC}< \widehat{BAC}\) (Cái khúc này không chắc, sai thì thôi)
c) Hướng dẫn:
\(\Delta\)EDB = \(\Delta\)FDC (cạnh huyền - góc nhọn)
Suy ra EB = FC. Từ đó suy ra AE = AF.
Suy ra tam giác AEF cân tại A suy ra \(\widehat{AEF}=\frac{180^o-\widehat{A}}{2}\) (1)
Mặt khác tam giác ABC cân tại A nên \(\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\) (2)
Từ (1) và (2) suy ra đpcm

tu ve hinh :
cau b la vuong goc phai k
a, tamgiac ABC can tai A(gt) => AB = AC va goc ABC = goc ACB (dn)
goc ADB = goc ADC do AD | BC (GT)
=> tamgiac ADB = tamgiac ADC (ch - gn)
=> BD = DC (dn)
b, xet tamgiac BHD va tamgiac CKD co : BD = DC (Cau a)
goc ABC = goc ACB (cau a)
goc BHD = goc DKC = 90 do HD | AB va HK | AC (gt)
=> tamgiac BHD = tamgiac CKD (ch - gn)
=> HD = DK (dn)
c, xet tamgiac AHD va tamgiac AKD co : AD chung
HD = DK (cau b)
goc AHD = goc AKD = 90 do HD | AB va HK | AC (gt)
=> tamgiac AHD = tamgiac AKD (ch - cgv)
=> tamgiac AHK can tai A (dn)
=> goc AHK = (180 - goc BAC) : 2
tamgiac ABC can tai A (gt) => goc ABC = (180 - goc BAC) : 2
=> goc AHK = goc ABC 2 goc nay dong vi
=> HK // BC (tc)
d, tu ap dung py-ta-go

a) BC^2= Ac^2+Ab^2=> Bc^2=74=> Bc=căn 74. b)vì Ad là phân giác nên góc BAE và góc FAC bằng 45. Hai tam giác ABE và AFC đều vuông và đều có 1 góc 45 nên => tam giác vuông cân. Câu c) AD vuông góc Ax ( hai tia phân giác trong và phan giác ngoài của cùng 1 góc thì vuông góc nhau). Xét 2 tam giác vuông FAK và FEC có. FA=FC( theo câu b). Góc FCE = AFK cùng phụ FEC( do Tg FEI vuôg tại I). Và FAK=EFC=90 => tg AFK=tgEFC(g.c.g)=> AK=EF. phiền bạn tự trình bày lại cho hợp lí. Chúc bạn học tốt

a)Áp dụng Định lý Pythagoras cho tam giác vuông ABC:AB2+AC2=BC2<=>BC2-AB2=AC2=>AC2=152-122=81=>AC=9
b) Xét \(\Delta\)DBM và \(\Delta\)DCM:
DMB=DMC=90
BM=CM( M là trung điểm BC)
DM:chung
=>\(\Delta\)DBM=\(\Delta\)DCM(c-g-c)=>DC=DB
Xét \(\Delta\)ACD:A=90=>DC>DA
Mà DC=DB(chứng minh trên)
Nên:AD<DB
c)Xét \(\Delta\)BCG:BA \(\perp\)CG;GM\(\perp\)BC
Mà BA cắt GM tại D
Nên: D là trực tâm tam giác BCG
Lại có:CH\(\perp\)GB
Suy ra: C;D;H thẳng hàng
c)Xét \(\Delta\)GBC:GM là đường cao đồng thời là đường trung tuyến
=>\(\Delta\)GBC cân tại G=>GM là đường phân giác
Xét \(\Delta\)GDA và \(\Delta\)GDH:
GAD=GHD=90
GD:chung
AGD=HGD
=>\(\Delta\)GAD=\(\Delta\)GDH(cạnh huyền- góc nhọn)
=>AD=HD=>DAH=DHA=(180-HDA)/2
Xét \(\Delta\)DBC:DC=DB(chứng minh trên)=>DCB=DBC=(180-BDC)/2
Do HDA=BDC(đối đỉnh)
Nên AHD=BCD
Mà C;H;D thẳng hàng(chứng minh trên)
Suy ra AH//BC

Gọi P là trung điểm của BE. Từ P kẻ 1 tia vuông góc với BE cắt đoạn AB tại Q.
Xét tam giác BEM: ^BME=900, P là trung điểm của BE => PM=PB (1)
Ta tính được ^QBP = ^ABC - ^EBC = 750-300 = 450
Mà PQ vuông góc PB => Tam giác BPQ vuông cân tại P=> BP=PQ (2)
Từ (1) và (2) => PM=PQ => Tam giác PQM cân tại P
Dễ thấy ^MPE=600 => ^QPM=^QPE+^MPE = 900+600=1500
=> ^PQM= (1800 - ^QPM)/2 = 150
=> ^BQM= ^PQM + ^BQP = 150+450 = 600
Xét tam giác ABC: ^ABC=750; ^ACB=450 => ^BAC=600
Từ đó ta có: ^BQM=^BAC. Mà 2 góc này so le trg => MQ // AC
Lại có M là trung điểm của BC => Q là trung điểm của AC
=> PQ là đường trung bình của tam giác ABE => PQ//AE
Do PQ vuông góc BE => AE vuông góc BE (Quan hệ //, vuông góc)
=> ^AEB=900 (đpcm).
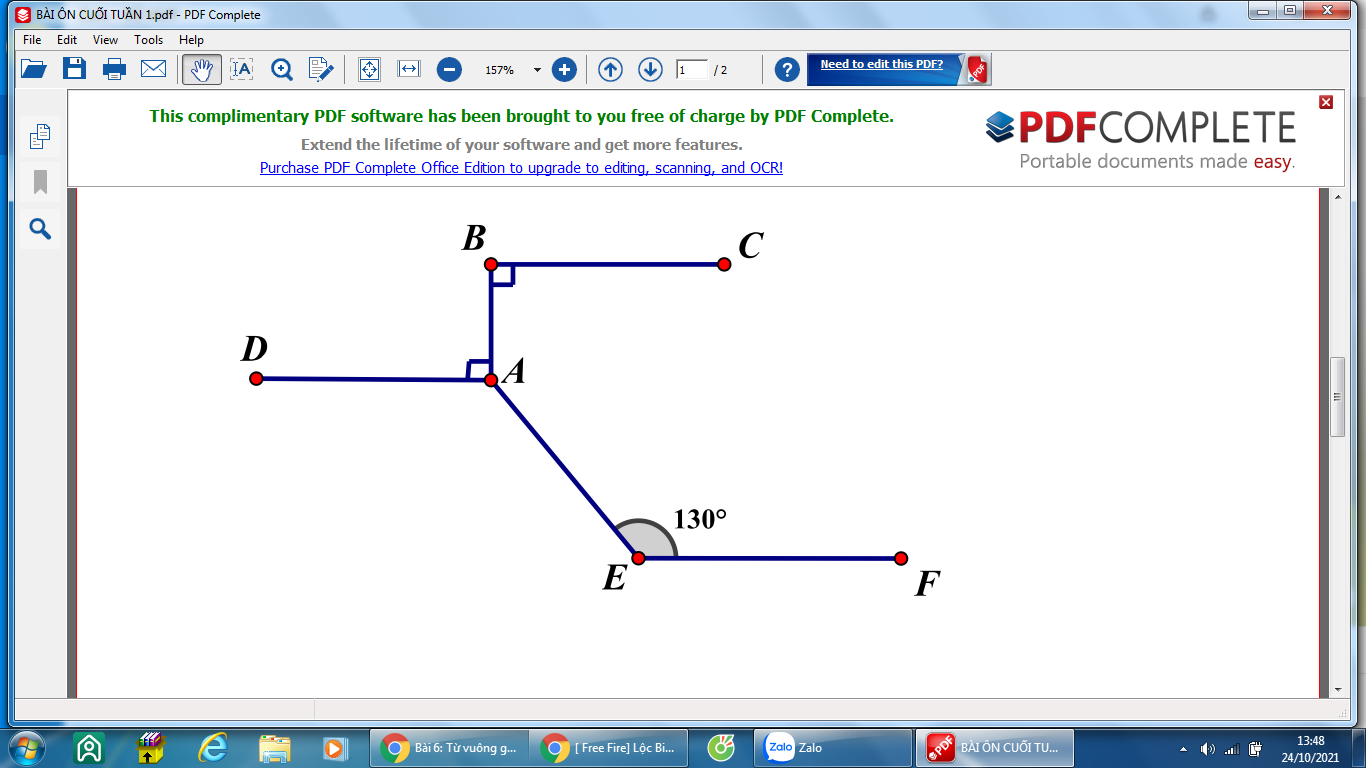
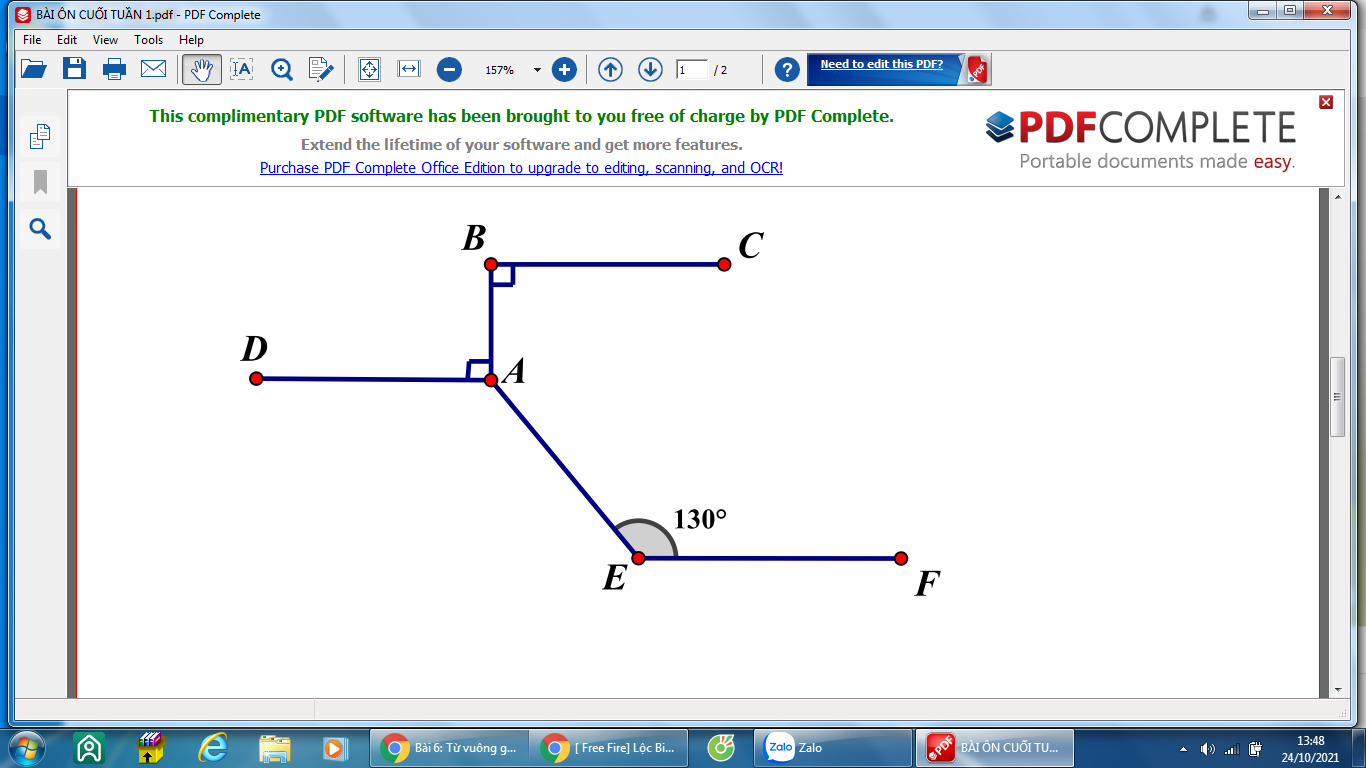
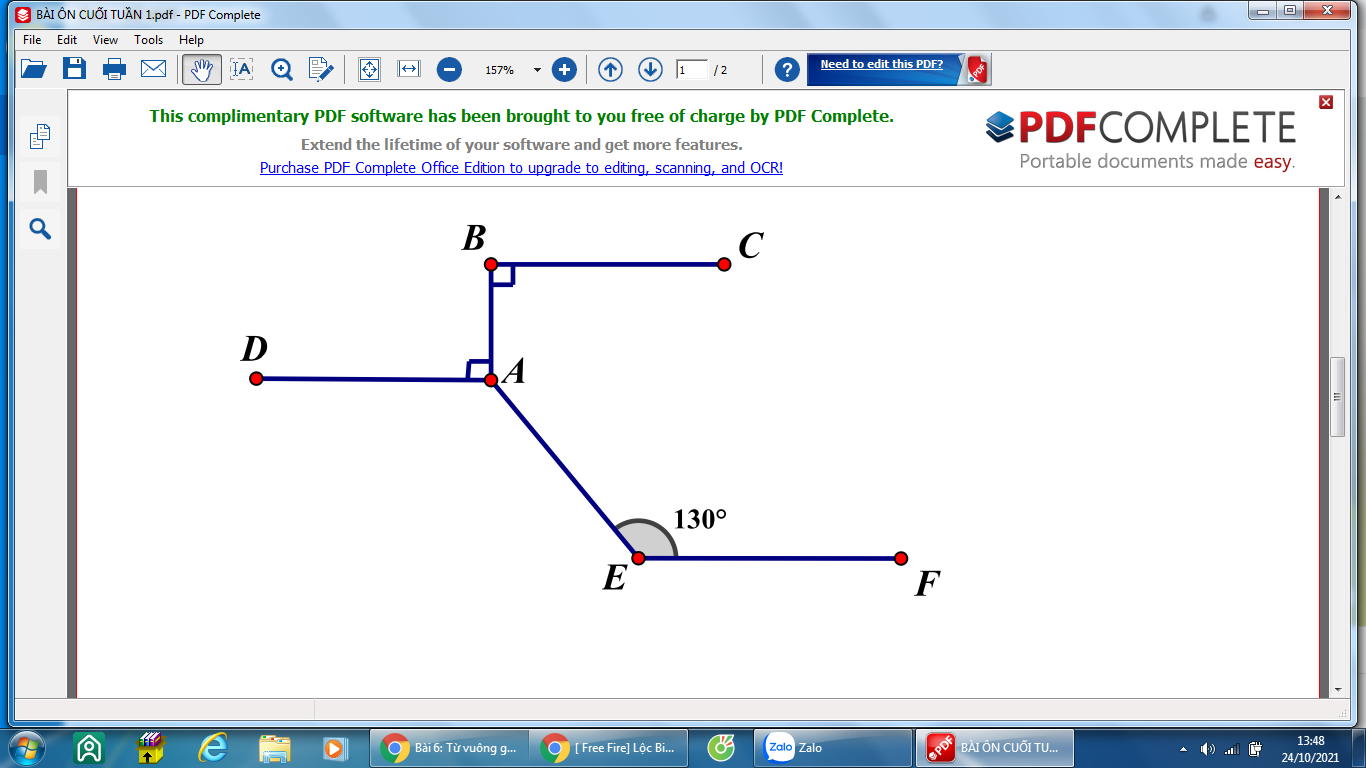
a, Vì BC và AD cùng vuông góc với AB nên BC//AD
Do đó AD//EF
b, \(\widehat{BAE}=360^0-\widehat{BAD}-\widehat{DAE}=360^0-90^0-130^0=140^0\)
Anh ko kẻ thêm à