Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hai tg AMC và tg ABC có chung đường cao từ C->AB nên
\(\dfrac{S_{AMC}}{S_{ABC}}=\dfrac{AM}{AB}=\dfrac{1}{3}\Rightarrow S_{AMC}=\dfrac{1}{3}xS_{ABC}\)
Hai tg AMN và tg AMC có chung đường cao từ A->CM nên
\(\dfrac{S_{AMN}}{S_{AMC}}=\dfrac{MN}{MC}=\dfrac{1}{2}\Rightarrow S_{AMN}=\dfrac{1}{2}xS_{AMC}=\dfrac{1}{2}x\dfrac{1}{3}xS_{ABC}=\dfrac{1}{6}xS_{ABC}\)
\(S_{BMC}=S_{ABC}-S_{AMC}=S_{ABC}-\dfrac{1}{3}xS_{ABC}=\dfrac{2}{3}xS_{ABC}\)
Hai tg BMN và tg BMC có chung đường cao từ B->MC nên
\(\dfrac{S_{BMN}}{S_{BMC}}=\dfrac{MN}{MC}=\dfrac{1}{2}\Rightarrow S_{BMN}=\dfrac{1}{2}xS_{BMC}=\dfrac{1}{2}x\dfrac{2}{3}xS_{ABC}=\dfrac{1}{3}xS_{ABC}\)
\(S_{ANB}=S_{AMN}+S_{BMN}=\dfrac{1}{6}xS_{ABC}+\dfrac{1}{3}xS_{ABC}=\dfrac{1}{2}xS_{ABC}=40cm^2\)
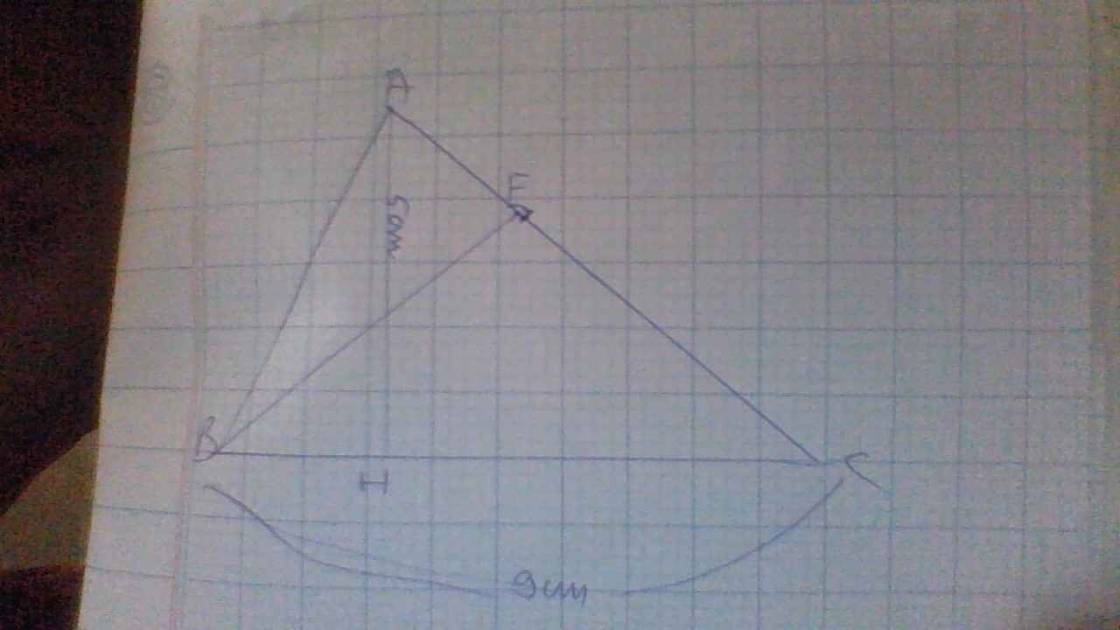

KHÓ QUÁ