Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình nói tóm tắt thôi nhé!
a) chứng minh được tam giác ABD = tam giác HBD (cạnh huyền - góc nhọn) => AD = DH (2 cạnh tương ứng)
b) tam giác HDC vuông tại H nên DC là cạnh lớn nhất => DC > DH; mà DH = AH (c/m trên) => DC > AD
c) Mình chưa nghĩ ra![]()
Câu c là tính HC nhé bạn!
c) Tính BC bằng cách dùng định lí pytago trong tam giác ABC, ta có: BC = 10cm
BH + HC = BC = 10cm
BH = AB = 6cm
=> HC = 10 - 6 = 4 cm
Chúc bạn học tốt!![]()

Xét tứ giác DHCN có
\(\widehat{DHN}=\widehat{DCN}=90^0\)
Do đó: DHCN là tứ giác nội tiếp
Suy ra: \(\widehat{HDC}=\widehat{HNB}\)
Xét ΔDHC và ΔNHB có
\(\widehat{DHC}=\widehat{NHB}\)
\(\widehat{HDC}=\widehat{HNB}\)
Do đó: ΔDHC∼ΔNHB

a,Ta có:AD vuông góc với BC(gt)
BE vuông góc với AD(gt)
Mà AD cắt BE tại H (gt)
Từ đó suy ra H là trực tâm
Mà H thuộc CH,suy ra CH vuông góc AB

a: Xét ΔAMD vuông tại M và ΔAND vuông tại N có
AD chung
\(\widehat{MAD}=\widehat{NAD}\)
Do đó: ΔAMD=ΔAND
Suy ra: AM=AN
b: Xét ΔABC có AD là đường phân giác
nên BD/AB=CD/AC
mà AB>AC
nên BD<CD

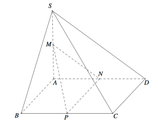

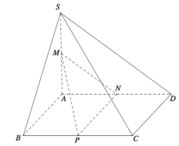

Bạn ơi bạn vẽ hình sai thì làm sao tụi mình c/m đc