Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAM và ΔBCN có
BA=BC
góc BAM=góc BCN
AM=CN
Do đó: ΔBAM=ΔBCN
=>BM=BN
=>ΔBMN cân tại B
b: DM+MA=DA
DN+NC=DC
mà DA=DC và MA=NC
nên DM=DN
BM=BN
DM=DN
Do đó: BD là trung trực của MN
=>BD vuông góc MN
c: Xét ΔABD có AB=AD và góc A=60 độ
nên ΔABD đều
ΔABD đều có BM là trung tuyến
nên BM là phân giác của góc ABD(1)
Xét ΔCBD có CB=CD và góc C=60 độ
nên ΔCBD đều
ΔCBD đều có BN là trung tuyến
nên BN là phân giác của góc DBC(2)
Từ (1), (2) suy ra góc MBN=1/2(góc ABD+góc CBD)
=1/2*góc ABC
=60 độ
Xét ΔBMN có BM=BN và góc MBN=60 độ
nên ΔBMN đều
=>góc BMN=60 độ

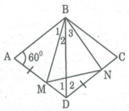
Nối BD, ta có AB = AD (gt)
Suy ra ∆ ABD cân tại A
Mà ∠ A = 60 0 ⇒ ∆ ABD đều
⇒ ∠ (ABD) = ∠ D 1 = 60 0 và BD = AB
Suy ra: BD = BC = CD
⇒ ∆ CBD đều ⇒ ∠ D 2 = 60 0
Xét ∆ BAM và ∆ BDN,ta có:
AB = BD ( chứng minh trên)
∠ A = ∠ D 2 = 60 0
AM = DN (giả thiết)
Do đó ∆ BAM = ∆ BDN ( c.g.c) ⇒ ∠ B 1 = ∠ B 3 và BM = BN
Suy ra ΔBMN cân tại B.
Mà ∠ B 2 + ∠ B 1 = ∠ (ABD) = 60 0
Suy ra: ∠ B 2 + ∠ B 3 = ∠ B 2 + ∠ B 1 = 60° hay ∠ (MBN) = 60 0
Vậy ∆ BMN đều

Vì \(\Delta ABD\)cân và có \(\widehat{A}=60^o\)nên là tam giác đều.
\(\Rightarrow AB=BD,\widehat{ABD}=\widehat{D_1}=60^o\)
\(\Rightarrow\widehat{D_2}=60^o\)
\(\Delta ABM=\Delta ABN\left(c.g.c\right)\)
\(\Rightarrow BM=BN;\widehat{B_1}=\widehat{B_3}\)
Lại có \(\widehat{B_1}+\widehat{B_2}=60^o\)nên \(\widehat{B_3}+\widehat{B_2}=60^o\)
Từ đó tìm số đo góc BMN là xong