Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Ta có:
$S_{ABD}=S_{ABC}$ (chiều cao bằng nhau và chung đáy $AB$)
$\Rightarrow S_{ADG}=S_{BCG}=129,9$ (cm2)
\(\frac{S_{ADG}}{S_{DCG}}=\frac{AG}{GC}=\frac{S_{ABG}}{S_{BGC}}=\frac{43,3}{129,9}=\frac{1}{3}\Rightarrow S_{DCG}=3\times S_{ADG}=3\times 129,9=389,7\)(cm2)
Diện tích hình thang $ABCD$ là:
$S_{ABG}+S_{BCG}+S_{ADG}+S_{DCG}=43,3+129,9+129,9+389,7=692,8$ (cm2)

Lời giải:
Ta có:
SABD=SABC����=���� (chiều cao bằng nhau và chung đáy AB��)
⇒SADG=SBCG=127,6⇒����=����=129,9 (cm2SADGSDCG=AGGC=SABGSBGC=31,9127,6=14⇒SDCG=4×SADG=4×127,6=510,4(cm2)��������=����=��������=43,3129,9=13⇒����=3×����=3×129,9=389,7(cm2)
Diện tích hình thang ABCD���� là:
SABG+SBCG+SADG+SDCG=31,9+127,6+127,6+510,4=797,5 (cm2)����+����+����+����=43,3+129,9+129,9+389,7=692,8 (cm2)

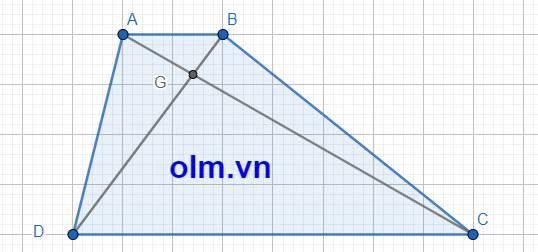
SABD = SABC (vì hai tam giác có hai chiều cao bằng nhau và chung đáy AB)
⇒ SABG + SADG = SABG + SBCG ⇒ SADG = SBCG = 179,2 cm2
Vì \(\Delta\)ABG và \(\Delta\)BCG có chung chiều cao hạ từ đỉnh B xuống đáy AC nên tỉ số diện tích \(\Delta\)ABG và \(\Delta\)BGC là tỉ số hai cạnh đáy:
\(\dfrac{AG}{GC}\) = \(\dfrac{44,8}{179,2}\) = \(\dfrac{1}{4}\)
Vì \(\Delta\)ADG và \(\Delta\)DCG có chung chiều cao hạ từ đỉnh D xuống đáy AC nên tỉ số diện tích \(\Delta\)ADG và \(\Delta\)DCG là tỉ số hai cạnh đáy:
\(\dfrac{AG}{GC}\) = \(\dfrac{1}{4}\)
⇒SDCG = SADG : \(\dfrac{1}{4}\) = 179,2 : \(\dfrac{1}{4}\) = 716,8 (cm2)
Diện tích của hình thang ABCD là:
44,8 + 179,2 + 179,2 + 716,8 = 1120 (cm2)
Đáp số: 1120 cm2

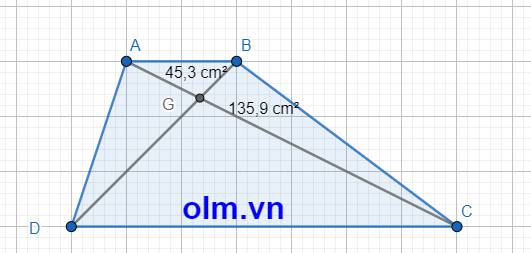
Hai tam giác ABD và tam giác ABC có chiều cao bằng nhau và chung cạnh đáy AB nên:
SABD = SABC = SABG + SBCG = SABG + SADG
⇒ SBCG = SADG = 135,9 cm2
Hai tam giác ABG và tam giác BGC có chung chiều cao hạ từ đỉnh B xuống đáy AC nên tỉ số diện tích hai tam giác là tỉ số hai cạnh đáy và bằng:
\(\dfrac{AG}{GC}\) = \(\dfrac{45,3}{135,9}\) = \(\dfrac{1}{3}\)
Hai tam giác ADG và tam giác DCG có chung chiều cao hạ từ đỉnh D xuống đáy AC nên tỉ số diện tích hai tam giác là tỉ số hai cạnh đáy và bằng:
\(\dfrac{AG}{GC}\) = \(\dfrac{1}{3}\) ⇒ SADG = \(\dfrac{1}{3}\)SDCG ⇒SDCG = 135,9\(\times\)3 = 407,7 (cm2)
Diện tích hình thang ABCD là:
45,3 + 135,9 + 135,9 + 407,7 = 724,8 (cm2)
Đáp số 724,8 cm2

Khối 6 của một trường có 4 lớp. Số học sinh 6A bằng \frac{11}{35}3511 tổng số học sinh ba lớp còn lại. Số học sinh 6B bằng \frac{17}{52}5217 tổng số học sinh ba lớp còn lại. Số học sinh 6C bằng \frac{6}{17}176 tổng số học sinh ba lớp còn lại. Số học sinh lớp 6D là 35 bạn. Hỏi số học sinh lớp 6A, 6B, 6C là bao nhiêu?
Đáp số: 6A : học sinh
6B : học sinh
6C : học sinh.
SABD = SABC (vì hai tam giác có chiều cao bằng nhau và chung cạnh đáy AB)
⇒ SABG + SADG = SABG + SBCG ⇒ SADG = SBGC = 170,8 cm2
\(\Delta\)ABG và \(\Delta\)BGC có chung chiều cao hạ từ đỉnh B xuống đáy AC nên tỉ số diện tích hai tam giác là tỉ số hai cạnh đáy và bằng:
\(\dfrac{AG}{GC}\) = \(\dfrac{42,7}{170,8}\) = \(\dfrac{1}{4}\)
\(\Delta\)AGD và \(\Delta\)DGC có chung chiều cao hạ từ đỉnh D xuống đáy AC nên tỉ số diện tích hai tam giác là tỉ số hai cạnh đáy và băng
\(\dfrac{AG}{GC}\) = \(\dfrac{1}{4}\)
⇒SDGC = SAGD : \(\dfrac{1}{4}\)
Diện tích tam giác DGC là: 170,8 : \(\dfrac{1}{4}\) = 683,2 (cm2)
Diện tích hình thang ABCD là:
42,7 + 170,8 + 170,8 + 683,2 = 1067,5 (cm2)
Đáp số: 1067,5 cm2