Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

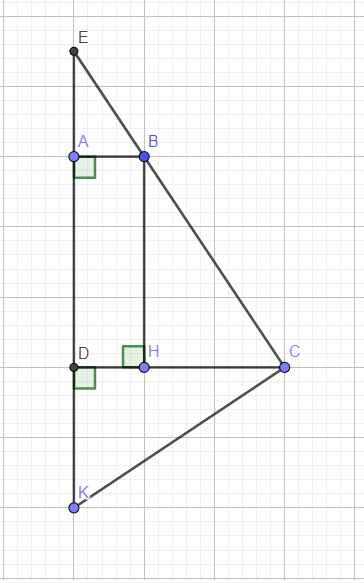
Do \(AD\perp CD\Rightarrow\) hình thang ABCD vuông tại A và D
\(\Rightarrow\) Tứ giác ABHD là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow AD=BH\) \(\Rightarrow BH=CD\)
Xét hai tam giác vuông BCH và CKD có:
\(\left\{{}\begin{matrix}BH=CD\\DK=CH\end{matrix}\right.\) \(\Rightarrow\Delta BCH=\Delta CKD\left(c.g.c\right)\) (1)
\(\Rightarrow\widehat{DCK}=\widehat{HBC}\)
\(\Rightarrow\widehat{BCK}=\widehat{BCH}+\widehat{DCK}=\widehat{BCH}+\widehat{HBC}=90^0\)
\(\Rightarrow BC\perp CK\)
b. Cũng từ (1) ta suy ra \(CB=CK\)
Áp dụng hệ thức lượng trong tam giác vuông ECK với đường cao CD:
\(\dfrac{1}{CD^2}=\dfrac{1}{CE^2}+\dfrac{1}{CK^2}=\dfrac{1}{CE^2}+\dfrac{1}{CB^2}\) (đpcm)

Gái xinh review app chất cho cả nhà đây: https://www.facebook.com/watch/?v=485078328966618 Link tải app: https://www.facebook.com/watch/?v=485078328966618
Kẻ đg cao BH của hình thang ABCD
Qua C kẻ đg thẳng ⊥ với CE cắt AD tại F
+ Tứ giác ABHD là HCN
=> BH = AD = CD
+ ΔBCH = ΔCFD ( g.c.g )
=> BC = CF
+ ΔCEF vuông tại C, đg cao CD
\(\Rightarrow\frac{1}{CD^2}=\frac{1}{CE^2}+\frac{1}{CF^2}\)
\(\Rightarrow\frac{1}{AD^2}=\frac{1}{CE^2}+\frac{1}{BC^2}\)

Bạn tự vẽ hình nhé.
Qua \(C\) vẽ đường thẳng vuông góc với \(CE\) cắt \(AD\) ở \(F\). Kẻ \(BH\perp CD,\) suy ra \(ABHD\) là hình chữ nhật. Do đó \(BH=AD=CD.\) Mặt khác \(\angle CFD=\angle BCH\) (cùng phụ với \(\angle DEC\)). Suy ra \(\Delta CDF=\Delta BHC\) (hai tam giác vuông bằng nhau theo trường hợp g.c.g). Thành thử \(CF=BC.\)
Xét tam giác vuông \(CEF\) có đường cao \(CD\), suy ra \(\frac{1}{CD^2}=\frac{1}{CF^2}+\frac{1}{CE^2}\to\frac{1}{AD^2}=\frac{1}{BC^2}+\frac{1}{CE^2}.\) (ĐPCM).

bài này ko khó nếu nắm rõ công thức
A)Ta có AD=DC ( giả thiết )
mà AD=BH ( cùng là chiều cao của hình thang)
=>BH=DC
=>Tam giác Dkc=Tam giác HCB (cạnh huyền cạnh góc vuông)
=>góc DKC=góc HCB (hai góc tương ứng )
mà Góc DKC+ góc DCK = 90 độ
=>góc HCB+ góc DCk=90
=>góc BCK=90 độ=> BC vuông góc với Ck
B )Tam giác ECK vuông tại C ( do câu a)
=>1/CD^2=1/EC^2+1/Ck^2
mà
Tam giác Dkc=Tam giác HCB (cạnh huyền cạnh góc vuông)
=> CK=CB
=>
1/CD^2=1/EC^2+1/CB^2