Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bài này ko khó nếu nắm rõ công thức
A)Ta có AD=DC ( giả thiết )
mà AD=BH ( cùng là chiều cao của hình thang)
=>BH=DC
=>Tam giác Dkc=Tam giác HCB (cạnh huyền cạnh góc vuông)
=>góc DKC=góc HCB (hai góc tương ứng )
mà Góc DKC+ góc DCK = 90 độ
=>góc HCB+ góc DCk=90
=>góc BCK=90 độ=> BC vuông góc với Ck
B )Tam giác ECK vuông tại C ( do câu a)
=>1/CD^2=1/EC^2+1/Ck^2
mà
Tam giác Dkc=Tam giác HCB (cạnh huyền cạnh góc vuông)
=> CK=CB
=>
1/CD^2=1/EC^2+1/CB^2


a) ΔADI và ΔCDL có: góc A = góc C = 90°
AD = CD (hai cạnh hình vuông)
góc D1 = góc D2
cùng phụ với góc CDI
Do đó ΔADI = ΔCDL (g.c.g)
Suy ra DI = DL. Vậy ΔDIL cân
b) Áp dụng hệ thức  là không đổi.
là không đổi.
Nhận xét: Câu a) chỉ là gợi ý để làm câu b). Điều phải chứng minh ở câu b) rất gần với hệ thức 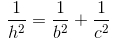
Nếu đề bài không cho vẽ DL ⊥ DK thì ta vẫn phải vẽ đường phụ DL ⊥ DK để có thể vận dụng hệ thức trên.

1. Ta có:
ED,EAED,EA là tiếp tuyến của (O)
→ED⊥OD,EA⊥OA⇒ˆADE=ˆOAE=90o→ED⊥OD,EA⊥OA⇒ADE^=OAE^=90o
EDOAEDOA có ˆADE+ˆOAE=180oADE^+OAE^=180o
⇒EDOA⇒EDOA nội tiếp đường tròn đường kính (OE)
→ˆDOA+ˆDEA=180o→DOA^+DEA^=180o
Mà ABCDABCD là hình thang cân
→ˆDMA=ˆDBA+ˆCAB=2ˆDBA=ˆDOA→DMA^=DBA^+CAB^=2DBA^=DOA^
→ˆDMA+ˆAED=180o→AEDM→DMA^+AED^=180o→AEDM nội tiếp được trong một đường tròn
2. Từ câu 1
→ˆEMA=ˆEDA=ˆDBA=ˆCAB→EMA^=EDA^=DBA^=CAB^
Vì EDED là tiếp tuyến của (O),ABCDABCD là hình thang cân
→EM//AB→EM//AB
3. Ta có:
EM//AB→HK//AB→HMAB=DMDB=CMCA=MKABEM//AB→HK//AB→HMAB=DMDB=CMCA=MKAB
→MH=MK→M→MH=MK→M là trung điểm HK


Do \(AD\perp CD\Rightarrow\) hình thang ABCD vuông tại A và D
\(\Rightarrow\) Tứ giác ABHD là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow AD=BH\) \(\Rightarrow BH=CD\)
Xét hai tam giác vuông BCH và CKD có:
\(\left\{{}\begin{matrix}BH=CD\\DK=CH\end{matrix}\right.\) \(\Rightarrow\Delta BCH=\Delta CKD\left(c.g.c\right)\) (1)
\(\Rightarrow\widehat{DCK}=\widehat{HBC}\)
\(\Rightarrow\widehat{BCK}=\widehat{BCH}+\widehat{DCK}=\widehat{BCH}+\widehat{HBC}=90^0\)
\(\Rightarrow BC\perp CK\)
b. Cũng từ (1) ta suy ra \(CB=CK\)
Áp dụng hệ thức lượng trong tam giác vuông ECK với đường cao CD:
\(\dfrac{1}{CD^2}=\dfrac{1}{CE^2}+\dfrac{1}{CK^2}=\dfrac{1}{CE^2}+\dfrac{1}{CB^2}\) (đpcm)