Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trong tứ giác ABCD, ta có: A+B+C+D=360° => A+120°+90°+60°=360° => A=360°-120°-90°-60°=90°

Mình lm tắt bạn tự hiểu nhé, ko hiểu chỗ nào thì hỏi mik
tam giác ADC= tam giác ABC (c.c.c)
=> A1=A2 (2 góc tg ứng)
=> AC là p/giác tam giác ADB (1)
Mà tam giác ABD cân do AD= AB ( giả thiết) (2)
từ (1) và (2) => AC là trung trực tam giác ADB
=> AClà trung trực BD (đpcm)
còn tính cái kia thì bạn lm theo hướng như sau
Vì tam giác ADC = tam giác ABC (cmt)
=> C1=C2= góc DCB :2 = 60 độ :2 = 30 độ
Còn A1=A2(cmt) => A1=A2=góc DAB:2 = 120 độ :2 = 60 độ
Xét tam giác ABC có tổng 3 góc = 180 độ r trừ đi góc A2 và góc C2 vừa tìm ra góc B= 90 độ
Vì tam giác ADC = tam giác ABC (cmt)
=> góc B= góc D ( 2 góc tg ứng) => góc D= 90 độ
Vậy D=B=90 độ


Ta có: ˆA+ˆB+ˆC+ˆD=360oA^+B^+C^+D^=360o
⇒ˆA+120độ+60độ+90độ=360độ⇒A^+120độ+60độ+90độ=360độ
⇒ˆA=360độ−90độ−60độ−120độ=90 độ

Vì \(AB//CD\) nên \(\widehat{A}+\widehat{D}=180^0\Rightarrow\widehat{A}=180^0-60^0=120^0\)
Ko đủ đề để tính \(\widehat{B};\widehat{C}\)

a) C−D=20o
Mà ta có C+D=360o−(A+B)=360o−(60o+90o)=210o (tổng 4 góc trong một tứ giác bằng 360o)
⇔C−D+C+D=20o+210o
⇔2C=230o
⇒C=115o và D=95o
Góc ngoài của tứ giác tại đỉnh C là 180o−115o=65o
Xét tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)( tổng các góc trong tứ giác)
\(\Rightarrow\widehat{C}+\widehat{D}=360^0-\widehat{A}-\widehat{B}=360^0-60^0-90^0=210^0\)
Ta có: \(\left\{{}\begin{matrix}\widehat{C}+\widehat{D}=210^0\\\widehat{C}-\widehat{D}=20^0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{C}=\left(210^0+20^0\right):2=115^0\\\widehat{D}=\left(210^0-20^0\right):2=95^0\end{matrix}\right.\)


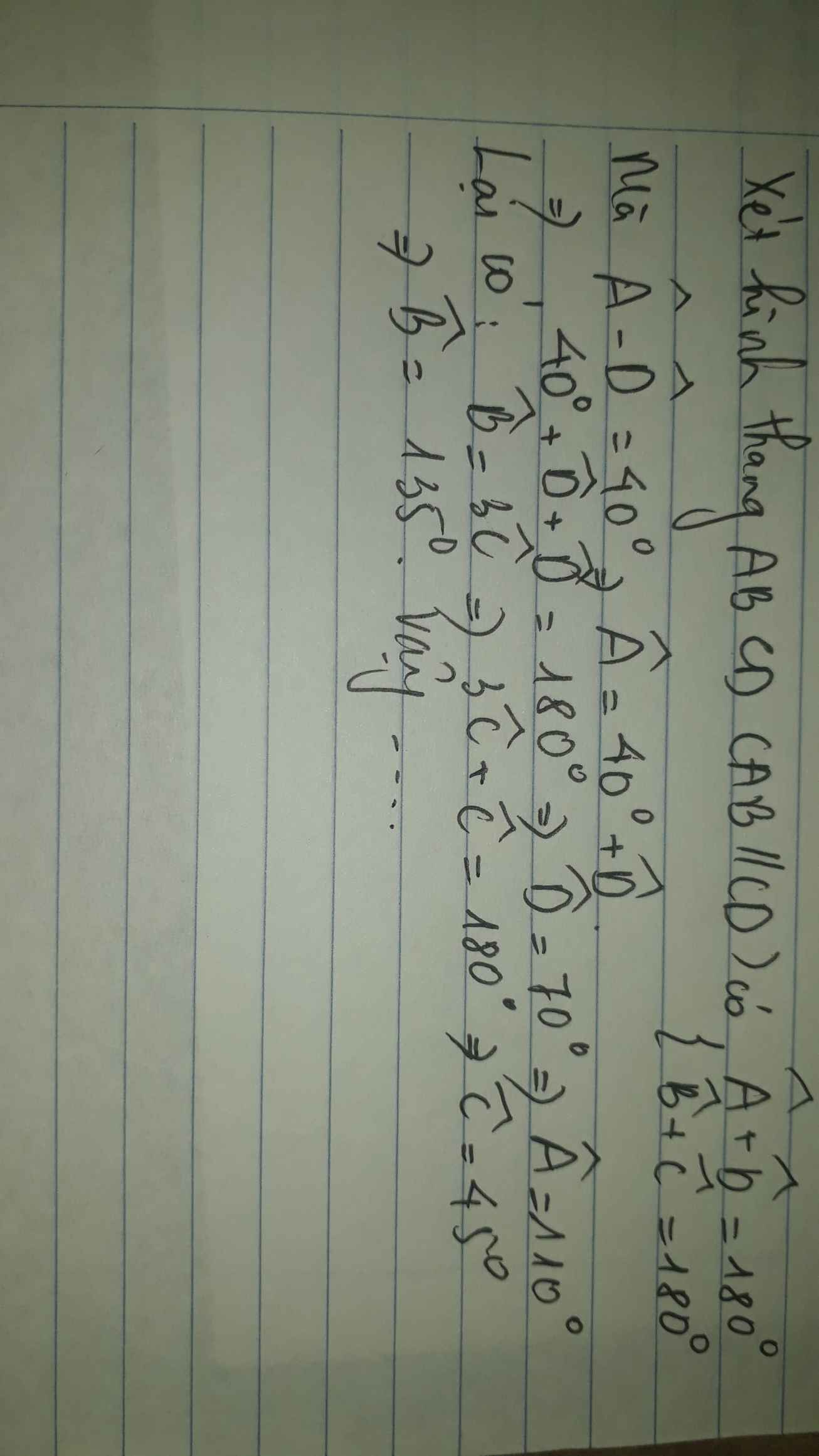
Vì tứ giác ABCD là hình thang và A B / / C D nên
A ^ + D ^ = 180 ° (hai góc kề một cạnh bên)
Mà A ^ = 120 ° nên D ^ = 180 ° − 120 ° = 60 °
Tương tự, B ^ + C ^ = 180 ° do đó C ^ = 60 °
Chọn A