Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔADC vuông tại D có
\(\tan\widehat{ACD}=\dfrac{AD}{DC}=\dfrac{1}{2}\)
nên \(\widehat{ACD}\simeq27^0\)
Áp dụng định lí Pytago vào ΔACD vuông tại D, ta được:
\(AC^2=AD^2+DC^2\)
\(\Leftrightarrow5\cdot AD^2=20\)
\(\Leftrightarrow AD=2\left(cm\right)\)
\(\Leftrightarrow DC=4\left(cm\right)\)
b: Xét ΔADC vuông tại D có DH là đường cao ứng với cạnh huyền AC nên ta có:
\(DH\cdot AC=DC\cdot DA\)
\(\Leftrightarrow DH\cdot2\sqrt{5}=2\cdot4=8\)
hay \(DH=\dfrac{4\sqrt{5}}{5}\left(cm\right)\)

a) Xét tam giác \(ADC\)vuông tại \(D\):
\(tan\widehat{ACD}=\frac{AD}{DC}=\frac{1}{2}\Rightarrow\widehat{ACD}=arctan\frac{1}{2}\)
b) Xét tam giác \(ADC\)vuông tại \(D\):
\(AC^2=AD^2+DC^2=AD^2+4AD^2=5AD^2\)
\(\Leftrightarrow AD=\sqrt{\frac{AC^2}{5}}=\sqrt{\frac{25^2}{5}}=5\sqrt{5}\left(cm\right)\)
\(AB=AD=5\sqrt{5}\left(cm\right),CD=2AD=10\sqrt{5}\left(cm\right)\).
c) Xét tam giác \(ADC\)vuông tại \(D\):
\(DH=\frac{AD.DC}{AC}=\frac{10\sqrt{5}.5\sqrt{5}}{25}=10\left(cm\right)\)
\(AH=\frac{AD^2}{AC}=\frac{AB^2}{AC}\Leftrightarrow\frac{AB}{AC}=\frac{AH}{AB}\)
Xét tam giác \(ABH\)và tam giác \(ACB\):
\(\widehat{A}\)chung
\(\frac{AB}{AC}=\frac{AH}{AB}\)
suy ra \(\Delta ABH~\Delta ACB\left(c.g.c\right)\)
\(\Rightarrow\widehat{ABH}=\widehat{ACB}\)

sai đề rồi nên không ai giúp đc tôi nghĩ 2a bình mới làm được câu c :)

c.
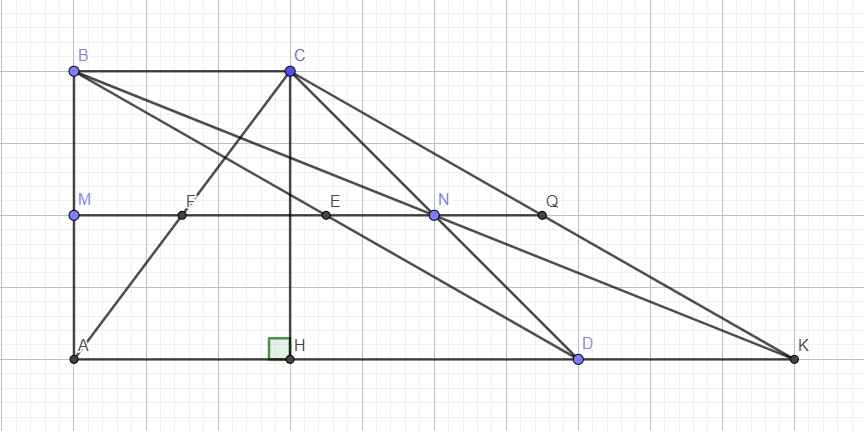
K thuộc AD nên BC song song DK
Áp dụng định lý Talet: \(\dfrac{BN}{KN}=\dfrac{CN}{DN}=1\Rightarrow BN=KN\) hay N là trung điểm BK
\(\Rightarrow\) BCKD là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Theo câu b, E, M, N thẳng hàng nên Q nằm trên MN (1)
Mà MN là đường trung bình của hình thang ABCD
\(\Rightarrow MN||AD\Rightarrow MN\perp AB\) (2)
Mà M là trung điểm AB (3)
(2);(3) \(\Rightarrow\) MN là trung trực AB (4)
(1);(4) \(\Rightarrow QB=QA\)
d.
Hạ CH vuông góc AD
Trong tam giác vuông CHK: \(cosKAC=\dfrac{AH}{AC}\Rightarrow AH=AC.cos\widehat{KAC}\)
Pitago: \(CH^2+AH^2=AC^2\)
Do đó: \(CK^2=CH^2+HK^2=CH^2+\left(AK-AH\right)^2=CH^2+AH^2+AK^2-2AK.AH\)
\(=AC^2+AK^2-2AK.AC.cos\widehat{KAC}\) (đpcm)
a.
\(tan\widehat{ACD}=\dfrac{AD}{CD}=\dfrac{1}{2}\Rightarrow\widehat{ACD}\approx26^034'\)
Áp dụng Pitago cho tam giác vuông ACD:
\(AC^2=AD^2+CD^2\Leftrightarrow\left(2\sqrt{5}\right)^2=AD^2+\left(2AD\right)^2\)
\(\Rightarrow AD^2=4\Rightarrow AD=2\Rightarrow AB=AD=2\)
\(CD=2AB=4\)
b.
Áp dụng hệ thức lượng trong tam giác vuông ACD:
\(DH.AC=AD.CD\)
\(\Rightarrow DH=\dfrac{AD.CD}{AC}=\dfrac{4.2}{2\sqrt{5}}=\dfrac{4\sqrt{5}}{5}\)