Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Qua A kẻ AE//BD (E Î DC)
Þ AE = BD = 12cm, DE = AB = 5cm
Þ DAEC vuông tại A (định lý Pytago đảo)
⇒ A H = A E . A C E C = 12.16 20 = 9 , 6 c m
Þ SABCD = 96cm2
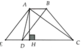

Kẻ BH ^ DC tại H.
Þ DBHC vuông cân tại H
Þ BH = 2cm
S A B C D = ( A B + D C ) . B H 2 = ( 1 + 3 ) .2 2 = 4 c m 2
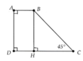

Kẻ BH ^ CD tại H Þ BH = B C 2 = 4cm.
Tính được SABCD = 22cm2

a) Chứng minh
DADH = DBCK (ch-gnh)
Þ DH = CK
Vận dụng nhận xét hình thang ABKH (AB//KH) có AH//BK Þ AB = HK
b) Vậy D H = C D − A B 2
c) DH = 4cm, AH = 3cm; SABCD = 30cm2
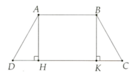
Kẻ BH ^ DC tại H Þ CH = 3cm.
Áp dụng định lý Pytago trong tam giác vuông BHC, suy ra BH = 4cm Þ SABCD = 18cm2