Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A, tam giác AOC vuông tại A
=> góc ACO + góc COA = 90 (đl) (1)
có góc COA + góc COD + góc DOB = 180
có góc COD = 90 (gt)
=> góc COA + góc DOB = 90 ; (1)
=> góc ACO = góc DOB
xét tam giác ACO và tam giác BOD có : góc CAO = góc OBD = 90 (gt)
=> tam giác ACO ~ tam giác BOD (g-g)
=> AC/BO = AO/BD
=> AO.BO = AC.BD
Có O là trung điểm của AB (gt) => AO = OB = 1/2AB
=> 1/2.AB.1/2.AB = AC.BD
=> 1/4AB^2 = AC.BD
=> AB^2 = 4AC.BD
b, tam giác CAO ~ tam giác OBD (Câu a)
=> AC/OB = OC/OD
OA = OB (Câu a)
=> AC/OA = OC/OD
=> AC/OC = OA/OD
=> tam giác ACOO ~ tam giác OCD
=> góc ACO = góc OCD
mà CO nằm giữa CA và CD
=> CO là phân giác của góc ACD (đn)
tự chứng minh AC = CM
c, xét tam giác AMB có : MO là đường trung tuyến (O là trung điểm của AB)
MO = AB/2 (OM = OA do tam giác AOC = tam giác MOC(câu b) và OA = AB/2)
=> tam giác AMB vuông tại M (định lí đảo)
=> AM _|_ NB (1)
xét tam giác ACM có : AC = CM (Câu b)
=> tam giác ACM cân tại C (đn) MÀ có CO là phân giác
=> CO là đường cao của tam giác ACM (đl)
=> CO _|_AM (2)
(1)(2) => CO // BN (tc)
xét tam giác BAN có : O là trung điểm của AB (gt)
=> C là trung điểm của AN (tc)
d, gọi BC cắt MH tại Q
có MH // AN do cùng _|_ BA
xét tam giác BCN và tam giác BCA
=> QM/CN = BQ/BC và QH/CA = BQ/BC (hệ quả)
có CN=CA (câu c)
=> MQ = QH ; Q nằm giữa H và M
=> Q là trung điểm của HM (đn)
kẻ AM cắt BD tại G; Kẻ OK _|_ AB (K nằm cùng 1 nửa mp bờ AB chứa Ax, By)
dài chẳng làm nữa

Năm sau tui thi THPT quốc gia rồi :v, không biết bạn Hoàng Hà còn cần câu này khum nhỉ?

a: BC=căn 6^2+8^2=10cm
AM là phân giác
=>MB/AB=MC/AC
=>MB/3=MC/4=10/7
=>MB=30/7cm; MC=40/7cm
b: Xét ΔAMC và ΔNMB có
góc MAC=góc MNB
góc AMC=góc NMB
=>ΔAMC đồng dạng với ΔNMB
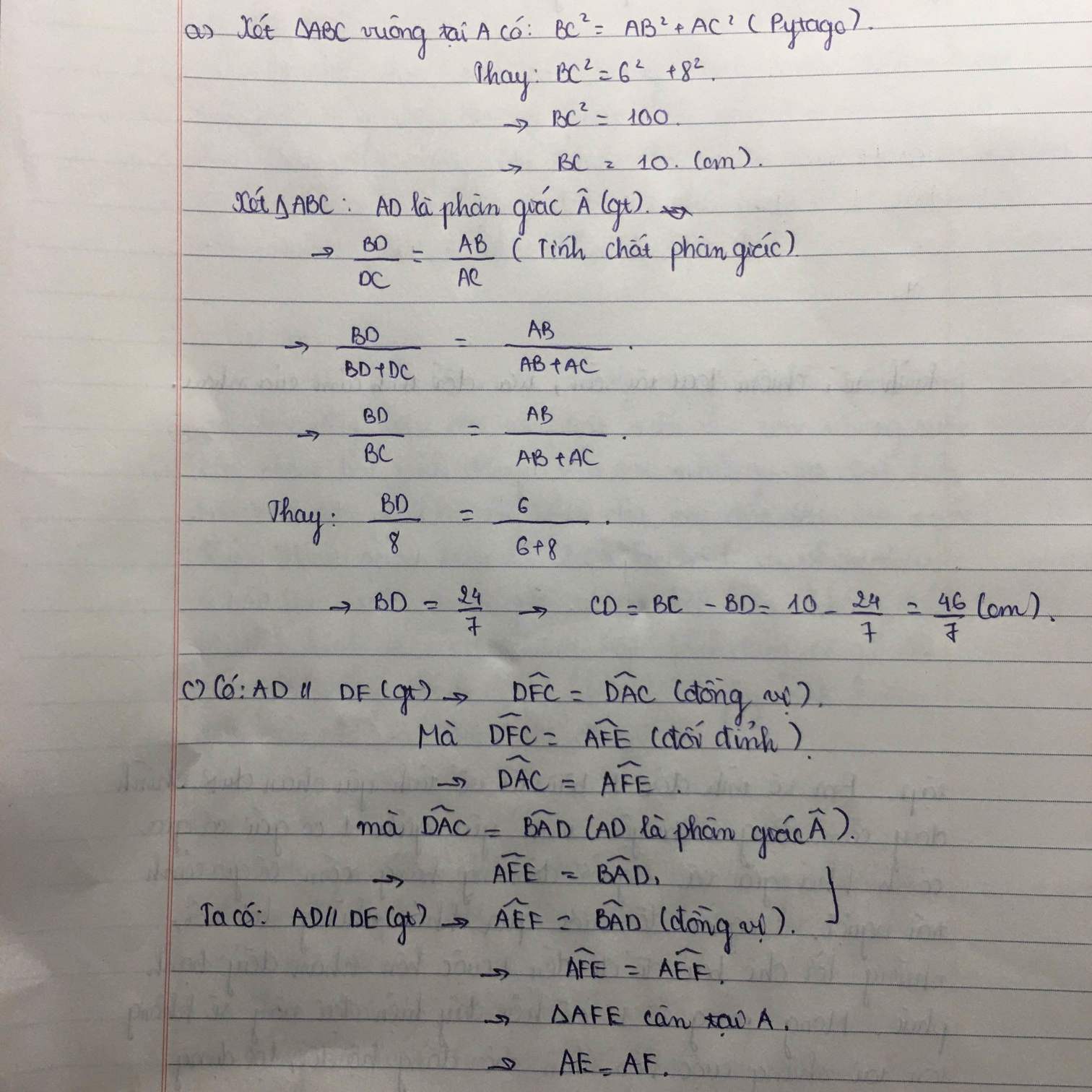

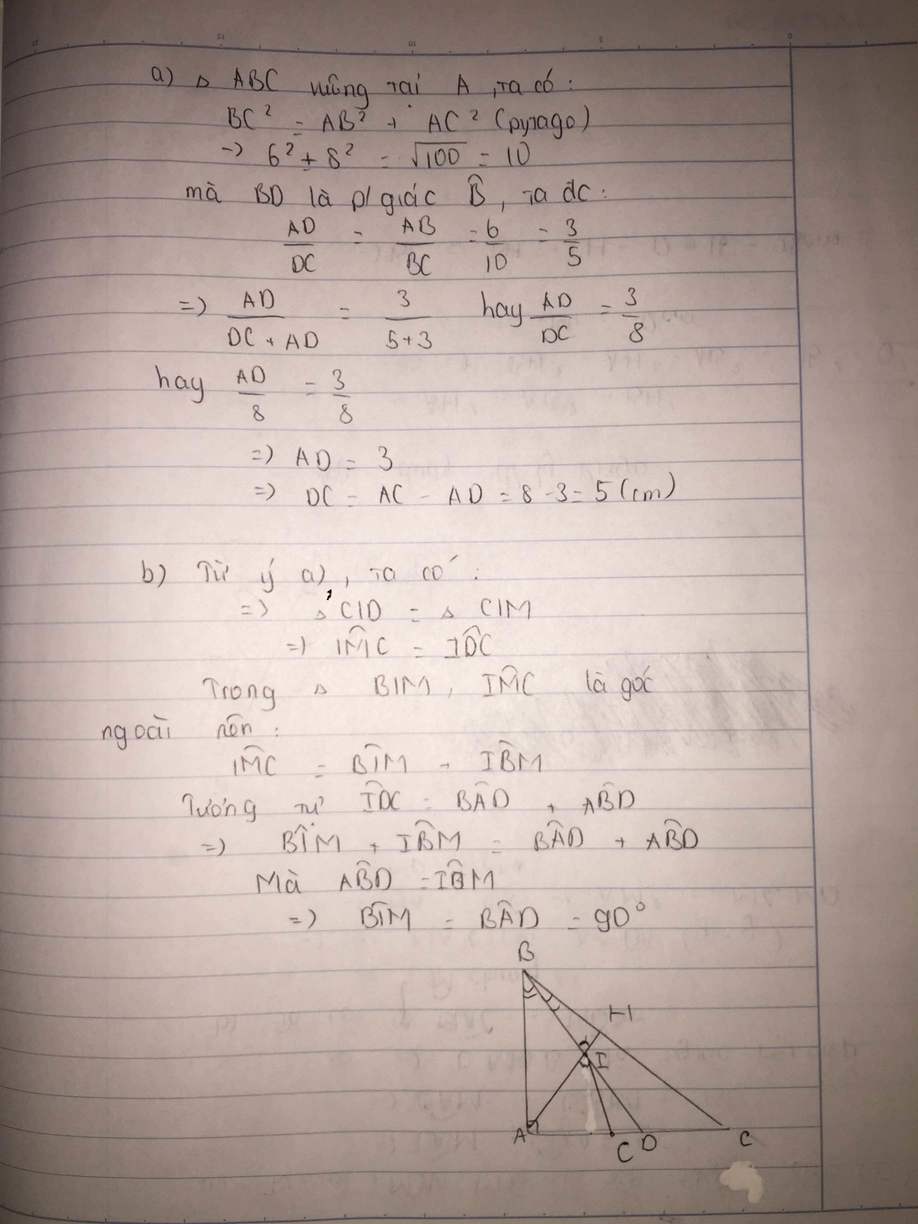
a, Vì AB // CD => \(\widehat{ABD}\)= \(\widehat{ODC}\), \(\widehat{BAD}\) =\(\widehat{OCD}\)(SLT)
Nên ΔAOB ᔕ ΔCOD (g.g)
Vì AB // CD => \(\dfrac{OA}{OC}=\dfrac{OB}{OD}=\dfrac{AB}{CD}=\dfrac{4}{8}=\dfrac{1}{2}\) = OB/OD = AB/CD (ĐL Ta-lét)
=> OA.OD =OB.OC
Ta có: OA = \(\dfrac{DC}{2}\) = \(\dfrac{6}{2}\) = 3 (cm)
b, Vì AB // DM => \(\dfrac{DM}{AB}=\dfrac{MI}{AI}\) (1)
Vì AB // MI => \(\dfrac{MC}{AB}=\dfrac{MK}{AB}\)(2)
Ta có: MD = MC (3)
(1), (2) và (3) => \(\dfrac{MI}{AI}=\dfrac{MK}{KB}\)<=> IK // AB ( Định lí Ta-lét đảo)
a: Xét ΔAOB và ΔCOD có
\(\widehat{AOB}=\widehat{COD}\)
\(\widehat{OAB}=\widehat{OCD}\)
Do đó: ΔAOB\(\sim\)ΔCOD
Suy ra: \(\dfrac{OA}{OC}=\dfrac{OB}{OD}=\dfrac{AB}{CD}\)
hay \(OA\cdot OD=OB\cdot OC\)
\(\dfrac{AB}{CD}=\dfrac{OA}{OC}\)
=>\(OA=\dfrac{4}{8}\cdot6=\dfrac{1}{2}\cdot6=3\left(cm\right)\)
b: