
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Vì \(\left\{{}\begin{matrix}AM=MD\\BN=NC\end{matrix}\right.\Rightarrow MN\) là đường trung bình hình thang ABCD
\(\Rightarrow MN=\dfrac{AB+CD}{2}\Rightarrow24=\dfrac{18+CD}{2}\\ \Rightarrow18+CD=48\\ \Rightarrow CD=30\left(cm\right)\)

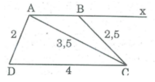
Phân tích: Giả sử hình thang ABCD dựng được thỏa mãn điều kiện bài toán.
Tam giác ADC dựng được vì biết ba cạnh AD = 2cm, DC = 4cm, AC = 3,5cm. Điểm B thỏa mãn hai điều kiện:
- B nằm trên đường thẳng đi qua A và song song với CD.
- B cách C một khoảng bằng 2,5cm.
Cách dựng:
- Dựng ∆ ADC biết AD = 2cm, DC = 4cm, AC = 3,5cm
- Dựng tia Ax // CD. Ax nằm trong nửa mặt phẳng bờ AD chứa điểm C.
- Dựng cung tròn tâm C bán kính 2,5cm. Cung này cắt Ax tại B, nối CB ta có hình thang ABCD cần dựng.
Chứng minh:
Tứ giác ABCD là hình thang vì AB // CD.
Hình thang ABCD có: AD = 2cm, CD = 4cm, AC = 3,5cm, BC = 2,5cm thỏa mãn yêu cầu bài toán.
Biện luận: Vì ∆ ADC luôn dựng được nên hình thang ABCD dựng được .
Vì cung tròn tâm C bán kính 3cm cắt Ax tại hai điểm nên ta dựng được hai hình thang thỏa mãn bài toán.

Kẻ BM//AD( \(M\in AD\))
Xét tứ giác ABMD có:
BM//AD(cách vẽ)
AB//DM( do AB//CD, \(M\in DC\))
=> Tứ giác ABMD là hình bình hành
=> AD=BM và AB=DM
Ta có: DM+MC=DC
=> AB+MC=DC
=> MC=DC-AB = 7-4=3cm
Xét tam giác BMC có:
BM + BC > MC( bất đẳng thức trong tam giác)
Mà BM=AD, MC= 4cm
=> AD+BC >4cm

Kẻ \(BE//AD\)
thì \(AD=BE\)
vÌ \(DE=AB=2cm\)
\(\Rightarrow EC=3cm\)
Xét tam giác BEC ta có :
\(BE+BC>EC=3cm\)
\(\Rightarrow AD+BC>3cm\) (đpcm)