Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

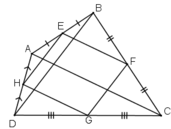
Ta có: EB = EA, FB = FC (gt)
⇒ EF là đường trung bình của ΔABC
⇒ EF // AC và EF = AC/2.
HA = HD, HC = GD
⇒ HG là đường trung bình của ΔADC
⇒ HG // AC và HG = AC/2.
Do đó EF // HG, EF = HG
⇒ EFGH là hình bình hành.
a) Hình bình hành EFGH là hình chữ nhật ⇔ EH ⊥ EF
⇔ AC ⊥ BD (vì EH // BD, EF// AC)
b) Hình bình hành EFGH là hình thoi
⇔ EF = EH
⇔ AC = BD (Vì EF = AC/2, EH = BD/2)
c) EFGH là hình vuông
⇔ EFGH là hình thoi và EFGH là hình chữ nhật
⇔ AC = BD và AC ⊥ DB.

Xét ΔABD có
E là trung điểm của AB
H là trung điểm của AD
Do đó: EH là đường trung bình của ΔABD
Suy ra: EH//BD và \(EH=\dfrac{BD}{2}\left(1\right)\)
Xét ΔBCD có
F là trung điểm của BC
G là trung điểm của CD
Do đó: FG là đường trung bình của ΔBCD
Suy ra: FG//BD và \(FG=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra EH//FG và EH=FG
hay EHGF là hình bình hành


Ta có : HE, GF lần lượt là đường trung bình của tam giác ADB và tam giác CDB
=> HE // BD, GF // BD và BD = 2HE = 2GF
Tương tự : HG, EF lần lượt là đường trung bình của tam giác DAC và tam giác BAC
=> HG // AC, EF // AC và AC = 2HG = 2EF
Nên EFGH là hình bình hành.
a) Đề hình bình hành EFGH là hình chữ nhật thì EH ⊥ EF => BD ⊥ AC
Điều kiện phải tìm : Hai đường chéo AC, BD vuông góc với nhau.
b) Để hình bình hành EFGH là hình thoi thì EH = EF => BD = AC
Điều kiện phải tìm : Hai đường chéo AC và BD bằng nhau.
c) Để hình bình hành EFGH là hình vuông thì EFGH phải vừa là hình chữ nhật, vừa là hình thoi => BD ⊥ AC và BD = AC.
Điều kiện phải tìm : Hai đường chéo AC, BD vuông góc với nhau và bằng nhau.

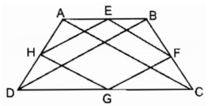
Trong ∆ ABD ta có:
E là trung điểm của AB (gt)
H là trung điểm của AD (gt)
nên EH là đường trung bình của ∆ ABD
⇒ EH // BD và EH = 1/2 BD (tính chất đường trung bình của tam giác) (1)
- Trong ∆ CBD ta có:
F là trung điểm của BC (gt)
G là trung điểm của CD (gt)
nên FG là đường trung bình của ∆ CBD
⇒ FG // BD và FG = 1/2 BD (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: EH // FG và EH = FG
Suy ra: Tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Trong ∆ ABC ta có:
EF là đường trung bình
⇒ EF = 1/2 AC (tính chất đường trung bình của tam giác) (3)
AC = BD (tính chất hình thang cân) (4)
Từ (1), (3) và (4) suy ra: EH = EF
Vậy : Tứ giác EFGH là hình thoi.

Vì E là trung điểm của AB
H là trung điểm của BC
=> EH là ĐTB của ^ABC
=> EH//AC và EH = 1/2.AC (1)
Vì F là trung điểm của AD
G là trung điểm của CD
=> FG là ĐTB của ^ADC
=> FG//AC và FG = 1/2.AC (2)
Từ (1) và (2) => EH//FG và EH = FG
=> EFGH là hình bình hành
a) Xét \(\Delta DAB\)có :
AE = EB (gt)
AF = FD (gt)
\(\Rightarrow\)EF là đường trung bình của \(\Delta DAB\)
\(\Rightarrow EF//BD;EF=\frac{1}{2}BD\left(1\right)\)
Xét \(\Delta BCD\)có :
BH = HC (gt)
CG = GD (gt)
\(\Rightarrow\)GH là đường trung bình của \(\Delta BCD\)
\(\Rightarrow GH//BD;GH=\frac{1}{2}BD\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow EF//GH;EF=GH\)
\(\Rightarrow\)Tứ giác EFGH là hình bình hành
b) Để EFGH là hình chữ nhật
\(\Rightarrow\widehat{FEH}=90^o\)
\(\Rightarrow FE\perp EH\)
Xét \(\Delta ABC\)có :
AE = EB (gt)
BH = HC (gt)
\(\Rightarrow\)EH là đường trung bình của \(\Delta ABC\)
\(\Rightarrow EH//AC\)
mà \(EH\perp EF\left(cmt\right)\)
\(\Rightarrow EF\perp AC\)
mà \(EF//BD\left(cmt\right)\)
\(\Rightarrow AC\perp BD\)
Vậy hình thang ABCD có điều kiện \(AC\perp BD\)thì EFGH là hình chữ nhật
Để EFGH là hình thoi
\(\Rightarrow EF=EH\)
Ta có : EH là đường trung bình của \(\Delta ABC\)
\(\Rightarrow EH=\frac{1}{2}AC\)
mà \(EF=\frac{1}{2}BD\)
và \(EH=EF\left(cmt\right)\)
\(\Rightarrow AC=BD\)
Vậy hình thang ABCD có điều kiện AC = BD thì EFGH là hình thoi