Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

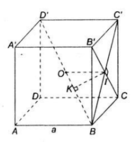
a) Ta có:
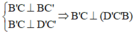
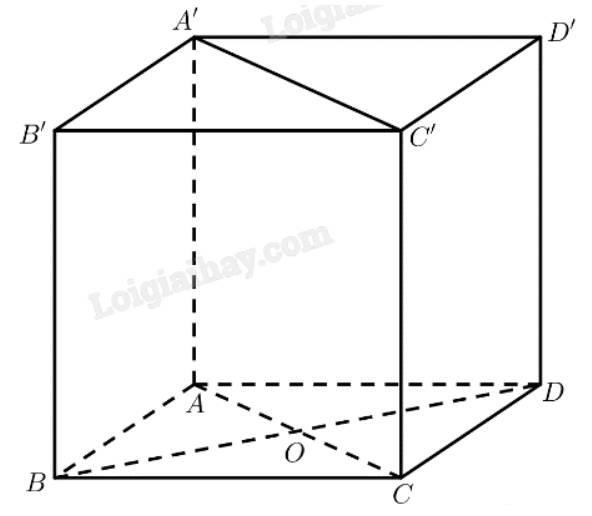
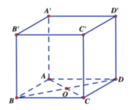
Gọi I là tâm hình vuông BCC'B'
Trong mặt phẳng (BC'D') vẽ IK ⊥ BD' tại K
Ta có IK là đường vuông góc chung của BD' và B'C
b) Gọi O là trung điểm của BD'
Tam giác BC’D’ có OI là đường trung bình nên :
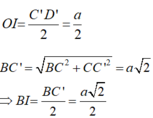
Vì ΔIOB vuông tại I có đường cao IK nên:
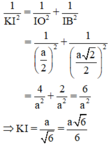

a) Gọi \(O = AC \cap B{\rm{D}}\)
\(ABCD\) là hình thoi \( \Rightarrow AC \bot B{\rm{D}} \Rightarrow AO \bot B{\rm{D}}\)
\(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AO\)
\( \Rightarrow d\left( {B{\rm{D}},AA'} \right) = AO = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\)
b) Tam giác \(OAB\) vuông tại \(O\)
\(\begin{array}{l} \Rightarrow BO = \sqrt {A{B^2} - A{O^2}} = \frac{a}{2} \Rightarrow B{\rm{D}} = 2BO = a\\{S_{ABC{\rm{D}}}} = \frac{1}{2}AC.B{\rm{D}} = \frac{{{a^2}\sqrt 3 }}{2}\\{V_{ABC.A'B'C'}} = {S_{ABC{\rm{D}}}}.AA' = \frac{{3{a^3}}}{4}\end{array}\)

\(\overrightarrow{DM}.\overrightarrow{A'N}=\left(\overrightarrow{DA}+\overrightarrow{AM}\right)\left(\overrightarrow{A'B'}+\overrightarrow{B'N}\right)\)
\(=\overrightarrow{DA}.\overrightarrow{A'B'}+\overrightarrow{AM}.\overrightarrow{A'B'}+\overrightarrow{DA}.\overrightarrow{B'N}+\overrightarrow{AM}.\overrightarrow{B'N}\)
( chứng minh được \(DA\perp A'B',AM\perp B'N\) )
\(=0+\dfrac{1}{2}\overrightarrow{AB}.\overrightarrow{AB}+\overrightarrow{C'B'}.\left(-\dfrac{1}{2}\overrightarrow{C'B'}\right)+0\)
\(=\dfrac{1}{2}AB^2-\dfrac{1}{2}C'B'^2=0\)
Suy ra \(DM\perp A'N\)
Ý A

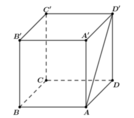
a) \(AA'C'C\) là hình chữ nhật
\(\left. \begin{array}{l} \Rightarrow AC\parallel A'C'\\A'C' \subset \left( {A'C'B} \right)\end{array} \right\} \Rightarrow AC\parallel \left( {A'C'B} \right)\)
\(ABC'D'\) là hình bình hành
\(\left. \begin{array}{l} \Rightarrow AD'\parallel BC'\\BC' \subset \left( {A'C'B} \right)\end{array} \right\} \Rightarrow AD'\parallel \left( {A'C'B} \right)\)
Ta có:
\(\left. \begin{array}{l}AC\parallel \left( {A'C'B} \right)\\AD'\parallel \left( {A'C'B} \right)\\AC,A{\rm{D}}' \subset \left( {AC{\rm{D}}'} \right)\end{array} \right\} \Rightarrow \left( {AC{\rm{D}}'} \right)\parallel \left( {A'C'B} \right) \Rightarrow \left( {\left( {AC{\rm{D}}'} \right),\left( {A'C'B} \right)} \right) = {0^ \circ }\)
b) Ta có:
\(\left. \begin{array}{l}AB\parallel A'B'\\A'B' \subset \left( {A'B'C'D'} \right)\end{array} \right\} \Rightarrow AB\parallel \left( {A'B'C'D'} \right) \Rightarrow \left( {AB,\left( {A'B'C'D'} \right)} \right) = {0^ \circ }\)

Đáp án C.