Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điểm A cách đều ba đỉnh, của tam giác đều A'BD vì ta có AB = AD = AA' = a, điểm C' cũng cách đều ba đỉnh của tam giác đều đó vì ta có :
\(C'B=C'D=C'A'=a\sqrt{2}\)


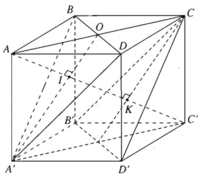
Điểm A cách đều ba đỉnh của tam giác đều A'BD vì ta có AB = AD = AA′ = a, điểm C' cũng cách đều ba đỉnh của tam giác đều đó vì ta có:
C′B = C′D = C′A′ = a√2
Vậy AC' là trục của đường tròn ngoại tiếp tam giác A'BD, tức là đường thẳng AC' vuông góc với mặt phẳng (A'BD) tại trọng tâm I của tam giác A'BD. Ta cần tìm khoảng cách A'I.
Ta có A′I = BI = DI = 2A′O/3 với O là tâm của hình vuông ABCD
Ta lại có 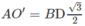
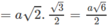
Vậy 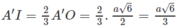
Tương tự điểm C' cách đều ba đỉnh của tam giác đều CB'D', tính được khoảng cách từ C, B', D' tới đường chéo AC'.

Lời giải:
a) Tứ giác DBB'D' là hình bình hành nên BD // B'D' . Vì vậy BD // (B'D'C) và BA' // CD' \(\Rightarrow\) BA' // ( B'D'C).
Từ đó suy ra ( BDA') //B'D'C).
b) Gọi ,
là giao điểm của AC' với A'O và CO'.
Do \(G_1=A'O\cap AI\) và A'O và AI là hai đường trung tuyến của tam giác nên \(G_1\) là trọng tâm của tam giác A'AC.
Chứng minh tương tự \(G_2\) là trọng tâm tam giác CAC'.
Suy ra \(\dfrac{AG_1}{AO}=\dfrac{2}{3}\); \(\dfrac{CG_2}{CO}=\dfrac{2}{3}\) nên đường chéo AC' đi qua trọng tâm của hai tam giác BDA' và B'D'C.
c) Do O và O' lần lượt là trung điểm của AC và A'C' nên \(OC=A'O'\) và OC' // A'O'.
Vì vậy tứ giác OCO'A là hình bình hành và OA'//OC.
Từ đó ta chứng minh được \(G_1\) lần lượt là trung điểm của \(AG_1\) và \(G_2\) là trung điểm của \(G_1C'\).
Do đó: \(AG_1=G_1G_2=G_2C\) (đpcm).
d) \(\left(A'IO\right)=\left(AA'C'C\right)\). Nên thiết diện cần tìm là (AA'C'C).

Đặt \(\overrightarrow{DA}=\)\(\overrightarrow{a}\) , \(\overrightarrow{DB}=\overrightarrow{b},\overrightarrow{DC}=\overrightarrow{c}\) với \(\left|\overrightarrow{a}\right|=\left|\overrightarrow{b}\right|=\left|\overrightarrow{c}\right|=a\) và \(\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{c}=\overrightarrow{c}.\overrightarrow{a}=\frac{a^2}{2}\) như hình vẽ
Do M là trung điểm AB nên \(\overrightarrow{DM}=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}\)
do đó \(\overrightarrow{CM}=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}-\overrightarrow{c}\)
Xét điểm \(N\in AC\), giả sử \(\overrightarrow{NA}=t.\overrightarrow{NC}\), \(t\ne1\). Khi đó \(\overrightarrow{DN}=\frac{\overrightarrow{a}-t\overrightarrow{c}}{1-t}\)
Vậy \(DN\perp CM\Rightarrow\overrightarrow{DN}.\overrightarrow{CM}=0\Leftrightarrow\left(\overrightarrow{a}+\overrightarrow{b}-2\overrightarrow{c}\right)\left(\overrightarrow{a}-t\overrightarrow{c}\right)=0\Leftrightarrow t=\frac{1}{2}\)
Từ đó , với \(N\in AC\) mà \(\overrightarrow{NC}=-2\overrightarrow{NA}\) thì \(DN\perp CM\) và khi đó
\(\overrightarrow{DN}=\frac{2}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{c}\)
Giả sử UV là đoạn vuông góc chung của CM, DN với \(U\in CM,V\in DN\) và \(\overrightarrow{CU}=u\overrightarrow{CM}=\frac{u}{2}.\overrightarrow{a}+\frac{u}{2}.\overrightarrow{b}-u.\overrightarrow{c},\overrightarrow{DV}=v.\overrightarrow{DN}=\frac{2v}{3}.\overrightarrow{a}+\frac{v}{3}.\overrightarrow{c}\)
Từ đó suy ra
\(\overrightarrow{UV}=\overrightarrow{DV}-\left(\overrightarrow{DC}+\overrightarrow{CU}\right)\)
\(=\left(\frac{2v}{3}-\frac{u}{2}\right)\overrightarrow{a}-\frac{u}{2}\overrightarrow{b}+\left(\frac{v}{3}+u-1\right)\overrightarrow{c}\)
Điều kiện \(\overrightarrow{UV}.\overrightarrow{CM}=0\) tương đương với :
\(\frac{1}{2}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{u}{4}-\left(\frac{v}{3}+u-1\right)+\frac{1}{4}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{1}{2}\left(\frac{2v}{3}-\frac{u}{2}\right)+\frac{u}{4}+\frac{1}{4}\left(\frac{v}{3}+u-1\right)+\frac{1}{4}\left(\frac{v}{3}+u-1\right)=0\)
Từ đó ta thu được \(u=\frac{2}{3}\)
Điều kiện \(\overrightarrow{UV}.\overrightarrow{DN}=0\) tương đương với :
\(\frac{2}{3}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{u}{6}+\frac{1}{3}\left(\frac{v}{3}+u-1\right)+\frac{1}{6}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{u}{12}+\frac{1}{3}\left(\frac{v}{3}+u-1\right)=0\)
Từ đó ta thu được \(v=\frac{6}{7}\)
Khi đó, \(\overrightarrow{UV}=\frac{5}{21}\overrightarrow{a}-\frac{7}{21}\overrightarrow{b}-\frac{1}{21}\overrightarrow{c}=\frac{1}{21}\left(5\overrightarrow{a}-7\overrightarrow{b}-\overrightarrow{c}\right)\)
Suy ra \(d\left(CM,DN\right)=UV=\sqrt{\left|\overrightarrow{UV}\right|^2}=\frac{a\sqrt{42}}{21}\)
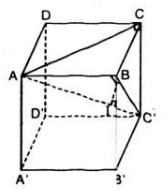




a) Ta có: ∆ ABC’ = ∆ C’CA = ∆ADC’=∆ AA’C’ =∆ C’B’A = ∆C’D’A (c.c.c)
⇒ Các đường cao hạ từ B; C; D; A’; B’; D’ xuống AC’ bằng nhau
( chú ý: các tam giác trên đều có chung cạnh AC’)
Gọi khoảng cách đó là h.
Ta có: CC’ = a;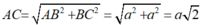
ΔC’AC vuông tại C, có hai cạnh góc vuông là CA và CC’. Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có: